Question

A solid cylinder of uniform density of radius $2cm$ has mass of $50g$. If its length is $12cm$, calculate its moment of inertia about an axis passing through its center and perpendicular to its length.

Answer 1

Hint: In the question they have asked the moment of inertia about the axis perpendicular to its length along with the axis passing through the centre, so use the theorem of perpendicular axes. It state that moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of its moment of inertia about two mutually perpendicular axes concurrent with perpendicular axis and lying in the plane of the laminar body. Use the formula of moment of inertia of a solid cylinder about the transverse or perpendicular axis passing through its centre. Moment of inertia about an axis passing through its center and perpendicular to its length depends upon mass of body, radius of body and length of body.

Complete step by step solution:

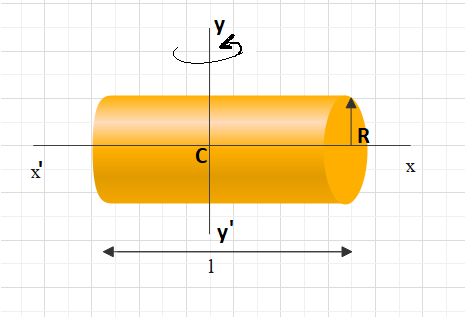
In the question it is given that a solid cylinder has uniform density that is having uniform thickness. A cylinder has radius $2cm$, has a mass of $50g$ . Length of cylinder is $12cm$.

Aim: Find moment of inertia about an axis passing through its centre and perpendicular to the length.

Since we need to calculate the moment of inertia about an axis perpendicular to its axis and centre. So we will use the theorem of the perpendicular axis.

This theorem states that the moment of inertia of plane lamina about an axis, perpendicular to its plane is equal to sum of its moment of inertia about any two mutually perpendicular axes concurrent with perpendicular axis and lying in the plane of laminar body.

We know that moment of inertia about an axis passing through its centre and perpendicular to its length is given by,

$I=\dfrac{M{{R}^{2}}}{4}+\dfrac{M{{l}^{2}}}{12}$

Where,

$I$ = moment of inertia
M= mass of uniform cylinder
R= radius of cylinder
l= length of cylinder

Put value given in question,

\[{{I}_{c}}=\dfrac{50\times {{10}^{-3}}\times {{(2\times {{10}^{-3}})}^{2}}}{4}+\dfrac{50\times {{10}^{-3}}\times {{(12\times {{10}^{-2}})}^{2}}}{12}=6.50\times {{10}^{-5}}kg{{m}^{2}}\]
So the moment of inertia of the cylinder about its axis passing through its centre and perpendicular to length is \[6.50\times {{10}^{-5}}kg{{m}^{2}}\].

Note: Note that density of cylinder is uniform, that is, thickness of cylinder is uniform. If the density of the cylinder gets changed then the value of moment of inertia may change. Note that in our answer the unit of mass is kg but in question the mass of the cylinder is in unit grams or g. so convert gram into kilogram. Do not get confused between the theorem of parallel axis and the theorem of perpendicular axis theorem. Parallel axis theorem states that moment of inertia about of a body about any axis is equal to sum of its moment of inertia about a parallel axis passing through its centre of mass and product of its mass and square of the perpendicular distance between the two parallel axes.