Question

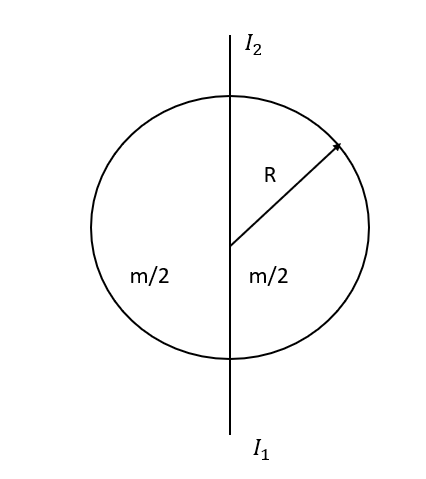
A solid hemisphere and a hemispherical shell are joined as shown. Both of them have $\dfrac{m}{2}$ individually. Find out the moment of inertia about axis $I_{1}$, $I_{2}$.

Answer 1

Hint: We have given the moment of inertia of a solid sphere and a hemispherical shell. Composite system is the combination of the solid sphere and hemispherical shell. The moment of inertia of the is the sum of the moment of inertia of the solid sphere and moment of inertia of the hollow sphere.

Complete step-by-step solution: -
Moment of inertia of the solid sphere, $I_{1} = \dfrac{2}{5} MR^{2}$.
Moment of inertia of the hollow sphere, $I_{2} = \dfrac{2}{3} MR^{2}$.
R is the radius.
The moment of inertia of a rigid composite system is the total moment of inertia of its component subsystems.
Moment of inertia,
$I = \dfrac{2}{3} MR^{2} + \dfrac{2}{5} MR^{2}$
$\implies I = \dfrac{16}{15} MR^{2}$
Given: $M = \dfrac{m}{2}$
$ I = \dfrac{16}{15} \times \dfrac{m}{2} \times R^{2}$
$\implies I = \dfrac{8}{15} MR^{2}$

Note: The moment of inertia is a quantity that defines the torque required for a desired angular acceleration around a rotational axis, how mass defines the force needed for the wanted acceleration. It depends on the body's mass configuration and the axis taken, with significant moments needing more torque to alter its rotation rate. It is an extensive property: the moment of inertia is just the mass times the perpendicular distance square to the pole of rotation. The moment of inertia of a complex composite system is the actual inertia of its component subsystems.