Question

A source of sound is travelling at $\dfrac{{100}}{3}m{s^{ - 1}}$ along a road, towards a point $A$. When the source is $3m$ away from $A$, a person standing at a point $O$ on a road perpendicular to the track hears a sound of frequency $f$. The distance of $O$ from $A$ at that time is $4m$. If the original frequency is $640Hz$, then the value of $f'$ is (given velocity of sound $ = 340m{s^{ - 1}}$)
A. $620Hz$
B. $680Hz$
C. $720Hz$
D. $840Hz$

Answer 1

Hint: In order to find the solution of the given question, first of all we need to find the component of the velocity in which it is acting. After that we need to apply the formula for the frequency according to the Doppler’s effect. Then we need to solve the equation obtained and finally we can conclude with the correct solution for the given question.

Complete step by step answer:
Step 1:
First of all let us draw a figure according to the given conditions.

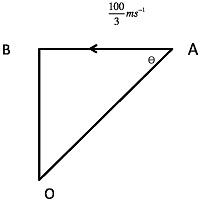
As we can see from the figure that the situation is of a right angle triangle, so we can find the hypotenuse which will be, $h = \sqrt {{3^2} + {4^2}} = \sqrt {25} = 5m$
Now, in the triangle, $\cos \theta = \dfrac{b}{h} = \dfrac{3}{5}$

Step 2:
Now, we need to find the horizontal component of the source of the sound as the sound is travelling along a road. So, we can write, ${v_s} = v\cos \theta = \dfrac{{100}}{3} \times \dfrac{3}{5} = 20m{s^{ - 1}}$

Step 3:
We know the formula for frequency in case of Doppler’s effect is given by,
$f' = f\left( {\dfrac{{v \pm {v_o}}}{{v \pm {v_s}}}} \right)$ -----(i)
Here, since the observer is not moving so the velocity of the observer is zero.
Now, putting the values in equation (i), we get,
$f' = 640\left( {\dfrac{{340 - 0}}{{340 - 20}}} \right)$
$ \Rightarrow f' = 640 \times \dfrac{{340}}{{320}} = 680Hz$
Therefore, the required value of the frequency is $680Hz$.

Hence, the correct answer is option (B).

Note: We define Doppler’s effect as the effect observed when either the source of a wave moves or the observer moves relative to each other. In other words we can say that the increase or decrease in the frequency of a wave when the source of the wave and the observer move towards or away from each other.