Question

A spherical conducting shell of inner radius ${r_1}$ and outer radius ${r_2}$ has a charge $Q$ . A charge $q$ is placed at the centre of the shell.
A.What is the surface charge density on the (i) inner surface (ii) outer surface of the shell?
B.Write an expression for the electric field at a point $x\, > {r_2}$ from the centre of the shell.

Answer 1

Hint: To approach the question, we have to draw the figure of the shell and label it with the given quantities. Now, we have to try to figure out how the charge will be induced on each part of the shell. With these induced charges, we apply the concept of charge density and Gauss’s Law. In the second part of the question, one should notice that the distance is $x$ and not ${r_2}$ . So, while solving the second part, put $x$ in the formula.
Formula used:
We can use Gauss’s Law as mentioned below:
$ \Rightarrow \oint {\overrightarrow E } .\widehat n\,dS = \dfrac{q}{{{\varepsilon _o}}}$
Where,
$E$ is the electric field.
$\widehat n$ is the outward drawn unit vector.
$S$ is the Gaussian surface.
$q$ is the charge.
${\varepsilon _o}$ is the permittivity of free space.

Complete answer:
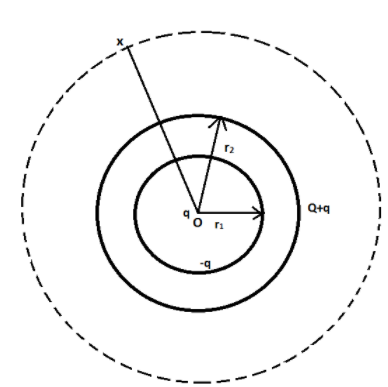
In the question, we have to identify the given quantities. It is given that the charge at the centre of the shell is $q$ and the charge on the outer shell having radius ${r_2}$ is $Q$ . Now, as the charge $q$ in the centre is positive in nature and the shell is conducting, the positive charge will induce a negative charge on the surface of the inner shell of radius, ${r_2}$ . This negative charge induced in the inner shell will further induce a positive charge on the outer shell. The induced positive charge will get added to the existing charge on the outer shell. Therefore the charge we get on the outer shell will be, $Q + q$ . With the help of the following figure, we can understand the problem in a better way.

Surface charge density can be defined as the charge per unit surface area. It measures the accumulation of electric charges in a given surface area. Its S.I. unit is $Coulomb\,{m^{ - 2}}$.
Mathematically, we can represent surface charge density by the formula given below:
$ \Rightarrow \sigma = \dfrac{q}{A}\,\,\,\,\,\,\,\,\,$ ----- 1
Where,
$\sigma $ is the surface charge density.
$q$ is the charge.
$A$ is surface area.
As the shell is spherical in shape, we get the surface area of the inner shell to be $4\pi {r_1}^2$ where ${r_1}$ is the radius of the inner shell and the charge on the inner shell is $ - q$ . So, we can put the value of the charge and surface area of the inner shell into equation (1), we get,
$ \Rightarrow \sigma = \dfrac{q}{A}$
$ \Rightarrow {\sigma _{inner}} = \dfrac{{ - q}}{{4\pi {r_1}^2}}$
Similarly, we can get the surface area of the outer shell to be $4\pi {r_2}^2$ where ${r_2}$ is the radius of the outer shell and the charge on the outer shell is $Q + q$ as explained earlier. So, we can calculate the surface charge density on the outer shell by using equation (1). Putting the values we get,
$ \Rightarrow \sigma = \dfrac{q}{A}$
$ \Rightarrow {\sigma _{outer}} = \dfrac{{Q + q}}{{4\pi {r_2}^2}}$
Now, let us assume $x$ to be a point outside the shell and to find the electric field at that point, we have to use Gauss’s Law. As the point is outside the shell, the entire shell can be considered as a point charge with the charge at its centre. Now, we can apply Gauss’s Law to find the electric field. Integrating the dot product of electric field,$E$ with outward drawn normal vector,$\widehat n$ over a closed curved surface, $dS$ , we get the following formula using Gauss’s Law:
\[\; \Rightarrow \oint {\overrightarrow E } .\widehat n\,dS = \dfrac{q}{{{\varepsilon _o}}}\,\,\,\,\,\,\,\,\] ---- 2
Where,
$E$ is the electric field.
$\widehat n$ is the outward drawn unit vector.
$S$ is the Gaussian surface.
$q$ is the charge.
${\varepsilon _o}$ is the permittivity of free space.
To apply Gauss’s Law, we have to draw a spherical Gaussian surface with $O$ as the centre and $x$ as the radius of the spherical surface as shown in the figure. The direction of the unit vector is radially outward and the electric field and the unit vector are in the same direction. Hence, we can deduce that the angle between them is zero. We know that the magnitude of the unit vector is unity. Therefore, to find the electric field at the distance $x$ from the centre, we have to use equation (2). Using equation (2) and integrating over the surface, $dS$ we get,
\[ \Rightarrow \oint {\overrightarrow E } .\widehat n\,dS = \dfrac{q}{{{\varepsilon _o}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\]
We know that the value of a unit vector is unity. Using the dot product formula between electric field and unit vector we get,
\[ \Rightarrow \int {E\cos \theta \,dS = } \dfrac{q}{{{\varepsilon _o}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\]
Where,
\[\overrightarrow { \Rightarrow E} .\widehat n = E\cos \theta \]
As the angle between the electric field and unit vector is zero and we know that the value of$\cos {0^o} = 1$ . So, putting the value in equation (3) we get,
\[ \Rightarrow \int {E\,dS = } \dfrac{q}{{{\varepsilon _o}}}\,\left( {\because \theta = {0^o}and\,\cos {0^o} = 1} \right)\,\,\]
As the electric field is uniform throughout the surface, we can take it out of the integration and integrate it over the surface area only. Therefore we get,
\[ \Rightarrow E\int {dS = } \dfrac{q}{{{\varepsilon _o}}}\,\]--- 4
Now, we know that the surface area of the Gaussian surface is $4\pi {x^2}$ and the total charge is $Q + q$ . Put the value of the surface area and the charge enclosed by the Gaussian surface in equation (4) and integrate them over the Gaussian surface we get the electric field at a point $x$to be,
\[ \Rightarrow E\int {dS = } \dfrac{q}{{{\varepsilon _o}}}\,\,\,\,\,\,\,\,\]
\[ \Rightarrow E \times 4\pi {x^2} = \dfrac{{Q + q}}{{{\varepsilon _o}}}\,\,\]
\[ \Rightarrow \,\,E = \dfrac{1}{{4\pi {\varepsilon _o}}}\dfrac{{Q + q}}{{{x^2}}}\]

Note:
The electric field inside a conductor is zero and the charge only reside on the surface.
According to Gauss’s Law, the flux of electrostatic field across a closed Gaussian surface is equal to the net charge enclosed by the Gaussian surface divided by permittivity of free space. It is used to determine the charge distribution and the electric field in the given charge distribution.