
A spherical of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r), is pressure at r (r < R), then the correct option(s) are:
A. P (r = 0) = 0
B.
C.
D.
Answer
486.6k+ views
Hint: Let g be the acceleration at the direction of the element at distance r from the centre O due to gravity. The difference in pressure (dp) on the two sides of the part in equilibrium is pressure by gravity per unit area.
Complete step by step answer:
So, we have
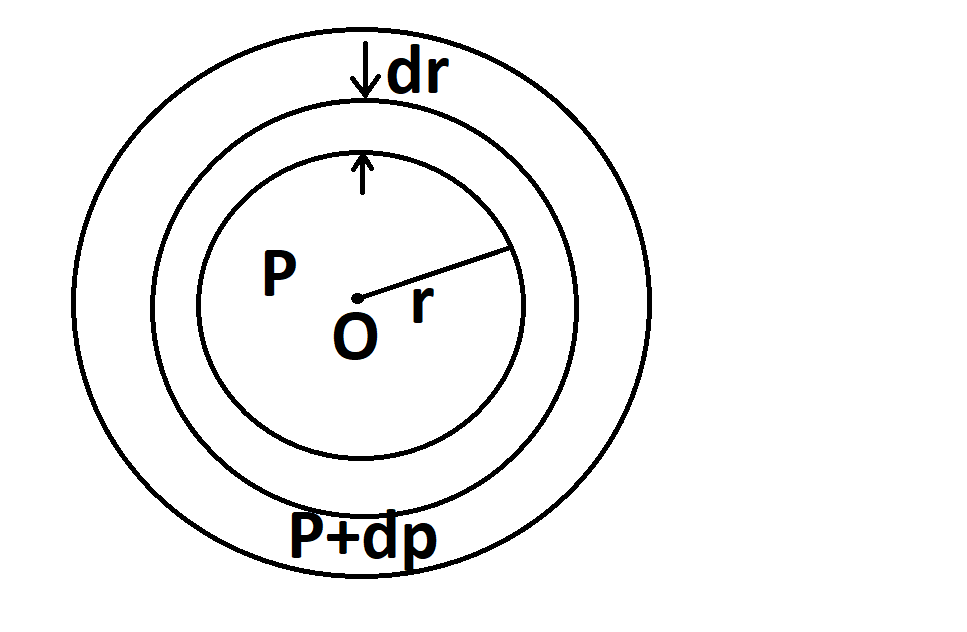
Now,
Let the mass of the spherical body with radius r be m
So, now
We have
Also,
By using the above values,
Integrating both side from P(=R) to P(=r)
We have
For,
P(R) = 0, we have P(r) =
Now,
When r = 0, P(r) =
For,
We have
Also,
We have
Now again
For,
Therefore, Option – B and Option – C are the correct relations, i.e.,
B.
C.
Note: In many instances, one may misunderstand the formula of buoyancy for the formula of pressure. Keep in mind that the formula for pressure uses height, whereas, the one for buoyancy uses volume.
Complete step by step answer:
So, we have

Now,
Let the mass of the spherical body with radius r be m
So, now
We have
Also,
By using the above values,
Integrating both side from P(=R) to P(=r)
We have
For,
P(R) = 0, we have P(r) =
Now,
When r = 0, P(r) =
For,
We have
Also,
We have
Now again
For,
Therefore, Option – B and Option – C are the correct relations, i.e.,
B.
C.
Note: In many instances, one may misunderstand the formula of buoyancy for the formula of pressure. Keep in mind that the formula for pressure uses height, whereas, the one for buoyancy uses volume.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




