
A spool of inner radius R and outer radius 3R has a moment of inertia
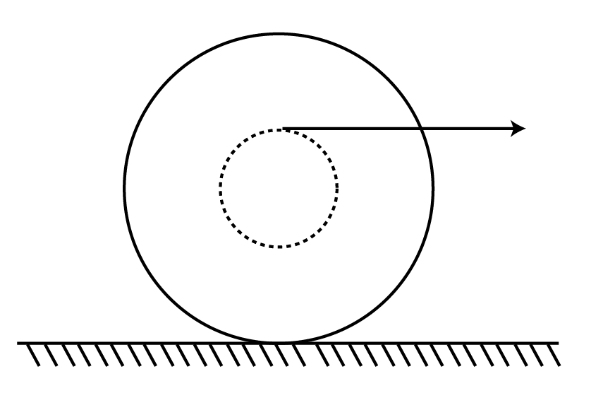

Answer
479.4k+ views
1 likes
Hint: We will first equate the torques acting on the spool about the center of rotation. Then by making use of parallel axis theorem we find the moment of inertia and obtain a relation between them. Substitute acceleration of center of mass in the angular acceleration formula, we can find the required answer.
Formula used:
Complete step by step answer:
The free body diagram of spool is given below
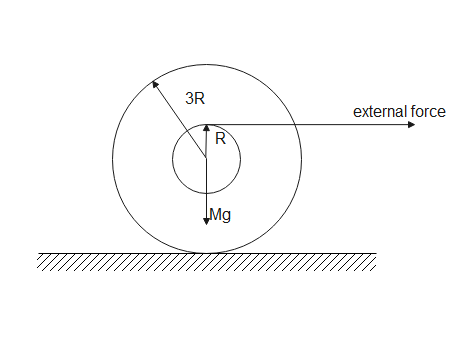
The external radius of the spool is R and internal radius is R.
Gravitational force acts on the body Mg in the download direction.
Now, let us equate the torques acting on the spool about the instantaneous center of rotation
Where I is the moment of inertia of the spool and
We will now use the parallel axis theorem, moment of inertia about the instantaneous center
Substituting in equation (1) we get
Now, we can write in terms of acceleration ‘a’ and radius
So, equation (2) becomes
Here, a is the acceleration of the center of mass.
Thus, the acceleration of the thread
Therefore, the acceleration of the point on the thread which is being pulled is
Note: Moment of inertia expresses a body's tendency to resist angular acceleration. It is equal to the “sum of the product of mass” of each particle with the “square of its distance from the axis of the rotation”. The formula for moment of inertia is
Formula used:
Complete step by step answer:
The free body diagram of spool is given below

The external radius of the spool is R and internal radius is R.
Gravitational force acts on the body Mg in the download direction.
Now, let us equate the torques acting on the spool about the instantaneous center of rotation
Where I is the moment of inertia of the spool and
We will now use the parallel axis theorem, moment of inertia about the instantaneous center
Substituting in equation (1) we get
Now, we can write in terms of acceleration ‘a’ and radius
So, equation (2) becomes
Here, a is the acceleration of the center of mass.
Thus, the acceleration of the thread
Therefore, the acceleration of the point on the thread which is being pulled is
Note: Moment of inertia expresses a body's tendency to resist angular acceleration. It is equal to the “sum of the product of mass” of each particle with the “square of its distance from the axis of the rotation”. The formula for moment of inertia is
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
EMI starts from ₹3,487.34 per month
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




