
A square field measures \[10\] meters by \[10\] meters. Ten students each mark a randomly selected region of the field; each region is square and has side lengths of \[1\] meter and no two regions overlap. The students count the earthworms contained in the soil to a depth of \[5\] centimeters beneath the ground’s surface in each region.
The results are shown in the table below.
Which of the following is a reasonable approximation of the number of earthworms to a depth of \[5\] centimeters beneath the ground’s surface in the entire field?
Region Number of earthworms Region Number of earthworms A \[107\] F \[141\] B \[147\] G \[150\] C \[146\] H \[154\] D \[135\] I \[176\] E \[149\] J \[166\]
(A) \[150\]
(B) \[1,500\]
(C) \[15,000\]
(D) \[1,50,000\]
| Region | Number of earthworms | Region | Number of earthworms |
| A | \[107\] | F | \[141\] |
| B | \[147\] | G | \[150\] |
| C | \[146\] | H | \[154\] |
| D | \[135\] | I | \[176\] |
| E | \[149\] | J | \[166\] |
Answer
461.4k+ views
Hint: In this question, we have to choose the required solution for the given particulars. We need to first find out the volume of the field with the depth given and secondly the volume of the region where each student count the earthworms contained in the soil then we divide the total volume by the total volume of the region where the earthworms are counted.Then we calculate the total number of earthworms and multiply with the derived number, thus we can easily find out the required solution.
Formula used: The volume of a cuboid is \[l \times b \times d\]
Where
l = the length of the cuboid
b = the breadth of the cuboid
d = the depth of the cuboid
Complete step-by-step solution:
It is given that a square field measures \[10\] meters by \[10\] meters. Ten students each mark a randomly selected region of the field; each region is square and has side lengths of \[1\] meter and no two regions overlap. The students count the earthworms contained in the soil to a depth of \[5\] centimeters beneath the ground’s surface in each region.
We need to find out the correct option which is a reasonable approximation of the number of earthworms to a depth of \[5\] centimeters beneath the ground’s surface in the entire field.
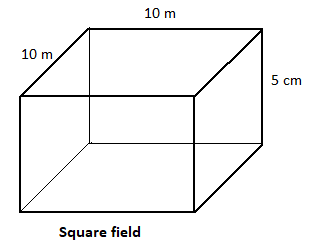
The volume of the square field measures \[10\] meters by \[10\] meters with depth of \[5\] centimeters beneath the ground’s surface is
\[ \Rightarrow 10 \times 10 \times .005{m^3}\] [Since one meter = \[100\]cm]
The volume of region selected by each student is \[1 \times 1 \times 0.005{m^3}\].
Then there will be \[\dfrac{{10 \times 10 \times .005}}{{1 \times 1 \times .005}} = 100\] such regions.
Thus the students have calculated for \[10\] such regions, it would be a good approximation to multiply the total number in these ten regions by \[10\] to get the total number of earthworms in the entire field.
Adding the calculated earthworms we get,
\[ \Rightarrow 107 + 147 + 146 + 135 + 149 + 141 + 150 + 154 + 176 + 166 = 1471\]
Thus the number of earthworms to a depth of \[5\] centimeters beneath the ground’s surface in the entire field is \[1471 \times 10 = 14,710\], which can be approximated to an order of \[15,000\].
$\therefore $ The option (C) is the correct answer.
Note: A cuboid is a three-dimensional shape with a length width, and height. The cuboid shape has six sides called faces. Each face of a cuboid is a rectangle, and all of a cuboid’s corners (called vertices) are 90-degree angles. Ultimately, a cuboid has the shape of a rectangular box.
Formula used: The volume of a cuboid is \[l \times b \times d\]
Where
l = the length of the cuboid
b = the breadth of the cuboid
d = the depth of the cuboid
Complete step-by-step solution:
It is given that a square field measures \[10\] meters by \[10\] meters. Ten students each mark a randomly selected region of the field; each region is square and has side lengths of \[1\] meter and no two regions overlap. The students count the earthworms contained in the soil to a depth of \[5\] centimeters beneath the ground’s surface in each region.
We need to find out the correct option which is a reasonable approximation of the number of earthworms to a depth of \[5\] centimeters beneath the ground’s surface in the entire field.

The volume of the square field measures \[10\] meters by \[10\] meters with depth of \[5\] centimeters beneath the ground’s surface is
\[ \Rightarrow 10 \times 10 \times .005{m^3}\] [Since one meter = \[100\]cm]
The volume of region selected by each student is \[1 \times 1 \times 0.005{m^3}\].
Then there will be \[\dfrac{{10 \times 10 \times .005}}{{1 \times 1 \times .005}} = 100\] such regions.
Thus the students have calculated for \[10\] such regions, it would be a good approximation to multiply the total number in these ten regions by \[10\] to get the total number of earthworms in the entire field.
Adding the calculated earthworms we get,
\[ \Rightarrow 107 + 147 + 146 + 135 + 149 + 141 + 150 + 154 + 176 + 166 = 1471\]
Thus the number of earthworms to a depth of \[5\] centimeters beneath the ground’s surface in the entire field is \[1471 \times 10 = 14,710\], which can be approximated to an order of \[15,000\].
$\therefore $ The option (C) is the correct answer.
Note: A cuboid is a three-dimensional shape with a length width, and height. The cuboid shape has six sides called faces. Each face of a cuboid is a rectangle, and all of a cuboid’s corners (called vertices) are 90-degree angles. Ultimately, a cuboid has the shape of a rectangular box.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Voters list is known as A Ticket B Nomination form class 9 social science CBSE

The largest brackish water lake in India is A Wular class 9 biology CBSE

The president of the constituent assembly was A Dr class 9 social science CBSE

What is the importance of natural resources? Why is it necessary to conserve them?

What are the causes of uneven distribution of population class 9 social science CBSE

Explain Right to Equality




