Question

A square plate of the side l has a mass per unit area \[\mu \]. Find the moment of inertia about an axis passing through the center and perpendicular to its plane

Answer 1

Hint: We can solve this problem by understanding the relationship between the dimensions, the mass per unit area, and the moment of inertia of an object. The dependence of moment of inertia on the axis under consideration has to be taken care of.

Complete step-by-step solution
We are given the dimension of a square plate and its mass per unit area. We have to find the moment of inertia along the axis passing through its center and perpendicular to its plane.
We know that the moment of inertia is defined as the effective mass of the rotating body along the axis of rotation. It is defined as the sum total of the masses from the center of mass along the axis. The moment of inertia is generally defined, mathematically, as –
\[I=M{{r}^{2}}\]
Where M is the mass of the body and r is the effective distance of the axis from the center of mass.
The value of ‘r’ changes with the shape, orientation, and plane under consideration of the object and the axis of rotation.
The moment of inertia along the center of the plate and perpendicular to the plane can be given by the perpendicular axis theorem. According to this theorem, the sum of the moment of inertias of two perpendicular axes is equal to the moment of inertia of a third axis which is perpendicular to the first two.

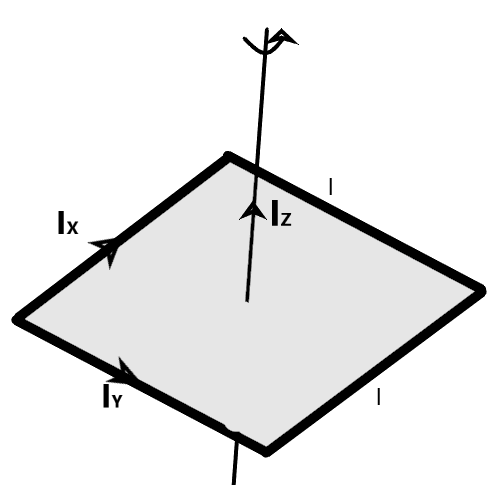
We know that the two perpendicular arms of the square plate along the X-axis and the Y-axis are equal to the moment of inertia of a long rod along its end. It is given as –
 \[{{I}_{X}}={{I}_{Y}}=\dfrac{M{{l}^{2}}}{12}\]
Now, we can find the mass of the square plate by using the mass per unit area and the side of the square as –
\[M=\mu {{l}^{2}}\]
Now, we can find the moment of inertia along the Z-axis, i.e., the axis passing through the center and perpendicular to its plane as –
\[\begin{align}
  & {{I}_{Z}}={{I}_{X}}+{{I}_{Y}} \\
& \Rightarrow {{I}_{Z}}=\dfrac{(\mu {{l}^{2}}){{l}^{2}}}{12}+\dfrac{(\mu {{l}^{2}}){{l}^{2}}}{12} \\
 & \therefore {{I}_{Z}}=\dfrac{\mu {{l}^{4}}}{6} \\
\end{align}\]
This is the required moment of inertia along the central perpendicular axis.

Note: The moment of inertia is the rotational analog of the mass. A body when rotating about an axis of its own will have different effective mass according to the position of the axis with respect to the orientation and the distance from the center of mass.