Question

A square tank of capacity 250 cubic m. has to be dug out. The cost of land is Rs. 50 per sq. m. The cost of digging increases with the depth and for the whole tank is 400 ${{\left( depth \right)}^{2}}$ rupees. Find the dimensions of the tank for the least total cost.
(a) $x=5,h=10$
(b) $x=\sqrt{5},h=50$
(c) $x=10,h=2.5$
(d) $x=\sqrt{10},h=25$

Answer 1

Hint: Use the dimensions of tank as height $=h$ , length and breadth $=x$. Then find the cost of area and depth separately and add them to have cost function. Then use the above relation to convert in terms of ‘h’ and hence, differentiate and equate it to 0 to find the value of h and find x.

Complete step-by-step answer:
In the question, we have been given a square tank of capacity 250 cubic meter has to be dug out. It is now further told that cost of land is Rs. 50 per sq. m. The cost of digging increases with the depth and for the whole tank is Rs. 400 ${{\left( depth \right)}^{2}}$ . We have to find the dimension for the least cost.
As we know the shape of a tank with a square base which means length and breadth are the same and height is different.
Let length be x, then breadth will also be x and let height be h.

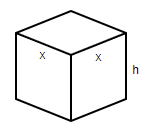
So, the volume of the tank will be $x \times x \times h$ $\Rightarrow {{x}^{2}}h$ by using the formula $Length\times breadth\times height$ .
We know that the volume of the tank is 250. So, ${{x}^{2}}h=250$
Now we will find an area of base which is equal to ${{x}^{2}}$ as the shape is square with length and breadth x.
Cost rate of land is Rs. 50 per sq. m.
So, cost of land is $50\times {{x}^{2}}=50{{x}^{2}}$
Cost rate of digging is Rs. 400 ${{\left( depth \right)}^{2}}$.
So, cost of digging with height h is Rs. $400{{h}^{2}}$
So, the total cost in terms of x and h is $400{{h}^{2}}+50{{x}^{2}}$ , let it be represented as C.
We know that ${{x}^{2}}h=250$, so we can substitute ${{x}^{2}}$ by $\dfrac{250}{h}$ in the expression of cost.
So, we can write expression of cost as
$ \Rightarrow C=400{{h}^{2}}+50{{x}^{2}}\times \dfrac{250}{h}$
In the question, we are asked to find dimensions such that it produces the least cost. So, for finding this we have to find the $\dfrac{dC}{dh}$ and equate it to 0.
So, for C to minimum,
$\dfrac{dC}{dh}=0$
At first we find $\dfrac{dC}{dh}$ so,
$ \Rightarrow C=400{{h}^{2}}+\dfrac{12500}{h}$
$ \Rightarrow \dfrac{dC}{dh}=800h-\dfrac{12500}{{{h}^{2}}}$
Now we will write $\dfrac{dC}{dh}=0$
On substituting the expression of $\dfrac{dC}{dh}$ we get,
$ \Rightarrow 800h-\dfrac{12500}{{{h}^{2}}}=0$
We can write it as,
$ \Rightarrow 800h=\dfrac{12500}{{{h}^{2}}}$
On doing cross multiplication and necessary simplification we get,
$ \Rightarrow {{h}^{3}}=\dfrac{125}{8}$
$ \Rightarrow h=\dfrac{5}{2}m$
Hence, the height of the tank is 2.5 m.
We know that ${{x}^{2}}=\dfrac{250}{h}$ . So now, substituting the value of h which is 2.5 m we get ${{x}^{2}}=100$ and hence, x is 10 m.
So, the value of x is 10 m.
The correct option is ‘C’.

So, the correct answer is “Option C”.

Note: After finding ‘h’ only they can check the option as in all the options dimensions are unique. So, there is no need for finding x to tick the correct option. Also, some students might try to use elimination methods by finding which option gives the capacity as 250 cubic m, but it will be in vain for these questions as all options will give 250 cubic m as the capacity.