Question

A stone is projected horizontally with a speed v from a height h above the ground. A horizontal wind is blowing in direction opposite to velocity of projection and gives the stone a constant horizontal acceleration of (direction opposite to initial velocity). As a result, the stone falls on ground at point vertically below the point of projection. Then find the value of \[\dfrac{{{f}^{2}}h}{g{{v}^{2}}}\](g is the acceleration due to gravity).

Answer 1

Hint: We need to consider the equations of motion of an object in two-dimensions to solve this problem. We can find relations between the given parameters and relate them together to reach the desired solution for the given expression.

Complete step by step answer:
In a projectile motion, an object is fired with a velocity that has its components along both the vertical and horizontal directions. In the situation given to us, the stone is projected horizontal, i.e., there is no vertical force and therefore, a vertical velocity or acceleration during the time of flight.
In a 2-D motion, the equation of motion can be given as –
\[S=ut+\dfrac{1}{2}g{{t}^{2}}\]
Where, S is the displacement along an axis,
u is the initial velocity,
g is the acceleration due to gravity,
t is the time of flight.
Let us consider our situation now. It is given that the stone has a horizontal velocity v at \[t=0\], at a height h.

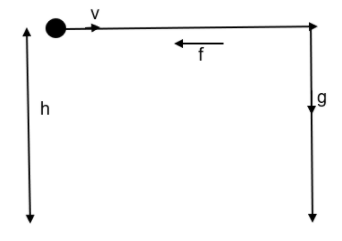
Due to the opposite horizontal force (acceleration f) the stone reaches an abrupt stop and falls vertically downwards under the force of gravity at an acceleration of g.
Applying the equation of motion, we get,
\[t=\sqrt{\dfrac{2h}{g}}\text{ --(1)}\]
Where h is the vertical height. The initial velocity is 0 at the start of vertical motion.
Also, at this point there is no more horizontal displacement.
The equation of motion for the horizontal motion becomes,
\[\begin{align}
  & 0=vt-\dfrac{1}{2}f{{t}^{2}} \\
 & \Rightarrow \text{ }vt=\dfrac{1}{2}f{{t}^{2}}\text{ } \\
 & \Rightarrow \text{ }t=\dfrac{2v}{f}\text{ --(2)} \\
\end{align}\]
Also, we have another equation for time of flight as in (1), So equating (1) and (2),
\[\begin{align}
  & \Rightarrow \text{ }\sqrt{\dfrac{2h}{g}}=\dfrac{2v}{f} \\
 & \Rightarrow \text{ }\dfrac{2h}{g}=\dfrac{4{{v}^{2}}}{{{f}^{2}}} \\
 & \Rightarrow \text{ }\dfrac{{{f}^{2}}h}{g{{v}^{2}}}=2 \\
\end{align}\]
So, the required answer is 2.

Note:
We can easily use this time of flight equation in 1-D for this question because here involves no parabolic motion after the horizontal flight. The stone tends to move down vertically at the instant when its initial velocity matches with the opposing velocity due to wind force.
The vertical motion is due to the cancelling of horizontal velocities.