Question

A stone is thrown vertically upwards with an initial velocity of 40m /s. Taking $g = 10m/{s^2}$, find the maximum height reached by the stone. What is the net displacement and the total distance covered by the stone?

Answer 1

Hint: When a ball is thrown vertically upwards, it initially moves upwards with the provided velocity and then comes back down. Solve this problem in two steps, first when the ball moves upwards and then when it free falls from its maximum height. Apply Newton’s third equation of motion to find the required physical quantity. And the total distance travelled by the ball will be the addition of distance covered when going up and coming down.

Formula Used:
Third equation of motion:
${v^2} - {u^2} = 2as$
where v is the final velocity of the object, u is the initial velocity of the object, a is the acceleration of the object, s is the displacement of the object.

Total distance,
h + h = 2h
where h is the maximum height obtained by the object.

Complete step-by-step answer:
When a stone is thrown vertically upwards with some initial velocity. It will move up until it reaches a certain point, known as the maximum height for that stone. Afterwards, it will start falling back down towards ground due to the gravitational force, g and will finally come back to its original place.

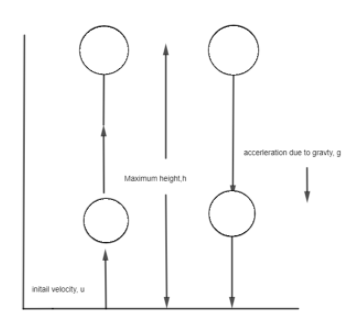
Given:
Initial velocity, $u = 40m/s$
Acceleration due to gravity, $g = 10m/{s^2}$
But because the stone is originally thrown upward the acceleration due to gravity would act in the direction opposite to its motion. So we will use negative signs for g.
i.e., $g = - 10m/{s^2}$
From the third equation of motion, we have:
${v^2} - {u^2} = 2as$
for our free falling stone we can write it as,
$\eqalign{
  & {v^2} - {u^2} = 2gh \cr
  & {\text{where }}g{\text{ is acceleration due to gravity,}} \cr
  & {\text{h is the height of the stone}}{\text{.}} \cr} $
When the stone reaches its maximum height, for a moment the velocity of the stone becomes zero at that instant and then it starts falling back towards ground.
So at maximum height, h:
$\eqalign{
  & v = 0 \cr
  & \Rightarrow 0 - {\left( {40} \right)^2} = 2 \times \left( { - 10} \right) \times h \cr
  & \Rightarrow - 1600 = - 20h \cr
  & \Rightarrow h = \dfrac{{ - 1600}}{{ - 20}} \cr
  & \Rightarrow h = 80m \cr} $
So, the maximum height to which the stone can reach is 80 m.

The total distance travelled by the stone would be the distance it covered while moving up and then the distance it covered while coming back down.
$\eqalign{
  & h = 80m \cr
  & \Rightarrow {\text{Total distance }} = 2h \cr
  & \therefore {\text{Total distance }} = 2 \times 80 = 160m \cr} $
Finally, because the stone is initially at the ground and after going up and then free falling comes down to the ground itself due to gravity. It comes back to its original position.
Displacement is defined as the change in the position of the moved object. In this case the stone comes back to its original position.
Therefore, $displacement, s = 0$.

Note:Students tend to make errors while solving these types of questions because they fail to apply the formulas correctly, as well as to use the correct sign based on the direction of motion of the object. So they should make sure to understand the problem’s scenario clearly and then solve it without any calculation error.