Question

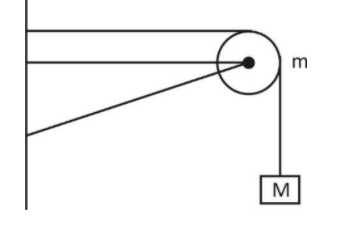
A string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by:

A. $\sqrt 2 Mg$
B. $\sqrt 2 Mg/k$
C. $g\sqrt {{{\left( {M + m} \right)}^2} + {m^2}} $
D. $g\sqrt {{{\left( {M + m} \right)}^2} + {M^2}} $

Answer 1

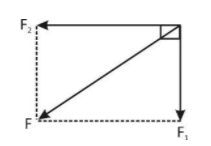
Hint: When two forces are acting at right angle, then resultant of the force is given by, \[F = \sqrt {{F_1}^2 + {F_2}^2} \]
The normal force always passes through the centre of the disc.
At equilibrium the not force into the system is zero.

Complete step by step solution:
Let tension in the string is T and force applied by pulley by the clamp is F. The free body diagram (FBD) of the system is given below:

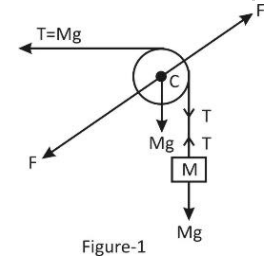
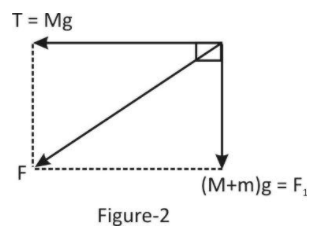
The total downward force into the system is ${F_1} = Mg + mg$ or ${F_1} = (M + m)g$ and the total horizontal force working on system is $T = Mg$ (see figure 1 and figure 2)
The force by pulley on clamp and by clamp on pulley will be equal and opposite.
Now, the resultant of vertical and horizontal force will be applied by clamp on pulley.
Now the force on the pulley by the clamp is given by from figure 2,
\[
  F = \sqrt {{F_1}^2 + {T^2}} \\
  F = \sqrt {{{\left[ {\left( {M + m} \right)g} \right]}^2} + {{\left( {Mg} \right)}^2}} \\
 \]
$
   = \sqrt {{{\left( {M + m} \right)}^2}{g^2} + {M^2}{g^2}} \\
  F = \left[ {\sqrt {{{\left( {M + m} \right)}^2}} + {M^2}} \right]g \\
 $

Hence, option (D) is correct.

Note: Note: The tension (T) in string is defined as “the force exerted by a string when it is subjected to pull”. Practically, if a person is holding a block of some weight attached to the one end of a staring then the force experienced by the person is Tension (T).