Question

A supersonic jet travelling at Mach 3.00 at an altitude of 20000 m is directly over a person at time t = 0 as shown in Figure.
How long will it be before the person encounters the shock wave?

Answer 1

Hint: In the question there is a jet travelling at mach 3.00. a person is standing directly under the jet. The height from the observer to the jet is given to us. We need to find the time taken for the shock wave to reach the observer. We know the equation to find the shock angle and from the figure we can find the change in position of the jet. Using this we can derive for velocity and thus get the time taken.

Formula used:
Shock angle,
$\sin \theta =\dfrac{v}{{{v}_{s}}}$
Velocity,
${{v}_{s}}=\dfrac{dx}{dt}$

Complete answer:
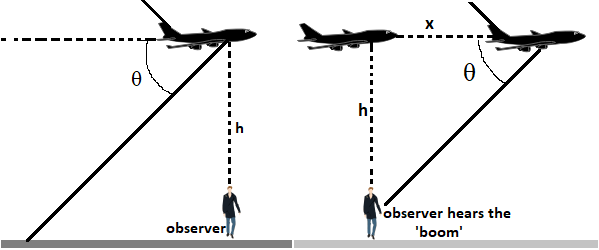
In the question it is said that a supersonic jet is travelling at an altitude ‘h’ and h is given to us.
h = 20000
The mach number of the jet is given to us as 3.00
We know that the average speed of sound in air is 335 m/s.

In the figure the angle ‘$\theta $’ is the shock angle.
We know the equation for the shock angle,
$\sin \theta =\dfrac{v}{{{v}_{s}}}$, where ‘$v$’ is the velocity of the sound in air and ‘${{v}_{s}}$’ is velocity of the mach.300
We know that velocity of mach is the product of Mach number and velocity of sound in air, i.e. ${{v}_{s}}=3\times 335$
Therefore we get,
$\begin{align}
  & \sin \theta =\dfrac{335}{3\left( 335 \right)} \\
 & \sin \theta =\dfrac{1}{3} \\
\end{align}$
From this we get the shock angle as,
$\begin{align}
  & \theta ={{\sin }^{-1}}\left( \dfrac{1}{3} \right) \\
 & \theta ={{19.47}^{o}} \\
\end{align}$
From the figure we get tan of the angle ‘$\theta $’ as,
 $\tan \theta =\dfrac{h}{x}$, where ‘h’ is the altitude of the jet and ‘x’ is the distance that the jet moves.
We know the value of ‘$\theta $’ and ‘h’, hence we can find ‘x’ as,
$x=\dfrac{h}{\tan \theta }$
$\begin{align}
  & x=\dfrac{20000}{\tan \left( 19.47 \right)} \\
 & x=5.6572\times {{10}^{4}}m \\
\end{align}$
This is the change in position of the jet.
We need to find the taken by the observer to hear the sound.
We now know that velocity is the derivative of position with respect to time.
Therefore here we have,
${{v}_{s}}=\dfrac{dx}{dt}$
In this above equation we know the values of ${{v}_{s}}$ and ‘x’, hence we get time as,
$dt=\dfrac{5.6572\times {{10}^{4}}}{335\times 3}$
$dt=56.29\sec $
This is the time taken by the observer to hear the shock wave.

Note:
When a wave is propagating and the medium of propagation does not change, then there is no change in the velocity of the sound wave. But if there is a relative motion between the source and the observer, then the frequency of the wave will change accordingly. This phenomenon is called the Doppler Effect in sound.
While solving the question we take velocity as the derivative of position with respect to time. In this case the change in position is the value marked as ‘x’ in the figure.