Question

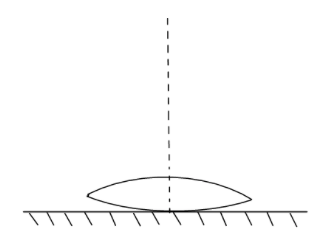
A symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5, is placed on top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y. Obtain the expression for the refractive index of the liquid in terms of x and y.

Answer 1

Hint: The combination of the lens have different focal length and also it is calculated differently using the formal known as Lens maker’s formula, the formula also involves refractive index of the lens. The focal length of the lens is always equal to the half of the radius of curvature.

Formula used:The formula of Lens maker’s is equal to,

$ \Rightarrow \dfrac{1}{f} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

Where focal length is f, the radius of curvature of lens 1 is ${R_1}$ and radius of curvature of lens 2 is ${R_2}$.
The formula of the combination of the lens is given by,

$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$

Where resultant focal length is f, the focal length of the lens 1 is ${f_1}$ and the focal length of the lens 2 is equal to ${f_2}$.

Complete step by step solution:
It is given in the problem that a symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5, is placed on top of a plane mirror as shown in the figure an optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself the distance of the needle from the lens is measured to be x, on removing the liquid layer and repeating the experiment, the distance is found to be y we need to obtain the expression for the refractive index of the liquid in terms of x and y.
The combination in which a biconvex lens is placed inside the liquid and liquid placed on the top of the plane mirror then this combination behaves as a combination of the convex lens and Plano concave lens where the focal length is ${f_1}$ and the focal length of the Plano concave lens is ${f_2}$.
The formula of the combination of the lens is given by,

$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$

Where resultant focal length is f, the focal length of the lens 1 is ${f_1}$ and the focal length of the lens 2 is equal to${f_2}$.
The focal length of the combination is equal to the $f = x$ and${f_1} = y$. The focal length ${f_2}$ is equal to,

$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
$ \Rightarrow \dfrac{1}{x} = \dfrac{1}{y} + \dfrac{1}{{{f_2}}}$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{1}{x} - \dfrac{1}{y}$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{{y - x}}{{xy}}$
$ \Rightarrow {f_2} = \dfrac{{xy}}{{y - x}}$.........eq. (1)

_{The formula for the Plano concave lens is given by,}

$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

One side of the lens is a plane mirror and therefore focal length is equal to infinity and the other side is concave which means the radius of curvature is equal to the $ - R$.
The refractive index is given as 1.5.

$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( { - \dfrac{1}{R} - \dfrac{1}{\infty }} \right)$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( { - \dfrac{1}{R}} \right)$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{{1 - n}}{R}$
$ \Rightarrow {f_2} = \dfrac{R}{{1 - n}}$………eq. (2)

Equating equation (1) and equation (2) we get.

$ \Rightarrow \dfrac{{xy}}{{y - x}} = \dfrac{R}{{1 - n}}$
$ \Rightarrow xy\left( {1 - n} \right) = R\left( {y - x} \right)$
$ \Rightarrow 1 - n = \dfrac{{R\left( {y - x} \right)}}{{xy}}$
$ \Rightarrow n = 1 - \dfrac{{R\left( {y - x} \right)}}{{xy}}$………eq. (3)

_{Applying the Lens maker’s formula for the convex lens part.}

$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {n - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

The radius of curvature is equal to${R_1} = R$, ${R_2} = - R$ and refractive index is 1.5.

$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {1 \cdot 5 - 1} \right)\left[ {\dfrac{1}{R} - \dfrac{1}{{\left( { - R} \right)}}} \right]$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {0 \cdot 5} \right)\left( {\dfrac{1}{R} + \dfrac{1}{R}} \right)$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \left( {0 \cdot 5} \right) \times \dfrac{2}{R}$
$ \Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{1}{R}$
$ \Rightarrow \dfrac{1}{y} = \dfrac{1}{R}$
$ \Rightarrow y = R$………eq. (4)

Replacing the value of equation (4) in equation (3) we get,

$ \Rightarrow n = 1 - \dfrac{{R\left( {y - x} \right)}}{{xy}}$
$ \Rightarrow n = 1 - \dfrac{{y \times \left( {y - x} \right)}}{{xy}}$
$ \Rightarrow n = \dfrac{{xy - y \times \left( {y - x} \right)}}{{xy}}$
$ \Rightarrow n = \dfrac{{xy - {y^2} + xy}}{{xy}}$
$ \Rightarrow n = \dfrac{{2xy - {y^2}}}{{xy}}$
$ \Rightarrow n = \dfrac{{2x - y}}{x}$.

The refractive index in terms of x and y is given by $n = \dfrac{{2x - y}}{x}$.

Note: The students are advised to understand and remember the formula of the combination of the lens formula and also the Lens maker’s formula as it is very useful in solving problems like these. The Plano concave lens is a convex lens in which one surface is plane and other is concave.