Question

A tangent \[PQ\] at a point \[P\] of a circle of radius \[5\] cm meets a line through the centre \[O\] at a point \[Q\] so that \[OQ = 13\] cm. Find the length of \[PQ\].

Answer 1

Hint: Here the given of the problem is the radius of a circle. As any tangent and the radius of a circle is perpendicular to each other. From the given information we will get a right-angle triangle. Then we will apply the Pythagoras theorem. From the theorem, we can find the length of \[PQ\].

Complete step-by-step answer:
It is given that; a tangent \[PQ\] at a point \[P\] of a circle of radius \[5\]cm meets a line through the centre \[O\] at a point \[Q\]so that \[OQ = 13\]cm.
          

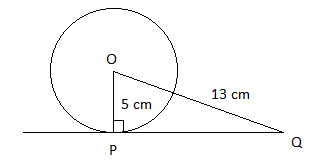
We have to find the length of \[PQ\].
We know that the tangent of a circle is perpendicular with its radius at the point of tangent.
So, here the radius \[OP\] is perpendicular to the tangent \[PQ\]. So, \[\angle OPQ = {90^ \circ }\].
Therefore, \[\Delta OPQ\] is a right-angle triangle whose \[\angle OPQ = {90^ \circ }\]and \[OQ = 13\]cm
So, we can apply Pythagoras theorem.
We have,
\[O{Q^2} = O{P^2} + P{Q^2}\]
Substitute the values we get,
\[{13^2} = {5^2} + P{Q^2}\]
Simplifying we get,
\[P{Q^2} = 169 - 25\]
Simplifying again we get,
\[PQ = \sqrt {144} = 12\] (we will take the positive value)
Hence, the length of \[PQ\] is \[12\] cm.

Note: Square root of any value gives two roots: one is positive and another is negative.
Here, \[PQ\] gives another value that is \[ - 12\]. But the length of any object cannot be negative. So, we ignore negative values for the length of \[PQ\].
Tangent to a circle is a line that touches the circle at one point, which is known as point of tangent. At the point of tangent, the tangent of a circle is always perpendicular to the radius.