
A test-tube shown in fig. has a diameter 20 mm and the height is 15 cm. The lower portion is a hemisphere. Find the capacity of the test tube.

(a) 26.05
(b) 46.05
(c) 16.05
(d) 36.05

Answer
495.6k+ views
Hint: In this question, from the diagram we can observe that the upper part is in the form of a cylinder and the bottom part is a hemisphere. Here, we need to find the height of the cylinder by the subtracting of the radius of the hemisphere from the height of the test tube. Now, we need to find the volume of the upper part using the formula for the volume of a cylinder given by
Complete step by step answer:
RIGHT CIRCULAR CYLINDER:
A right circular cylinder is considered a solid generated by the revolution of a rectangle about one of its sides.
The volume of a cylinder is given by the formula is given by
HEMISPHERE:
A plane passing through the center of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
The volume of a hemisphere is given by the formula
Now, from the given conditions in the question we have
Here, given the value of the diameter as
As we already know the relation between radius and diameter we get,
As we already know the relation between cm and mm is given as
Now, on simplifying further simplification and converting to cm we get,
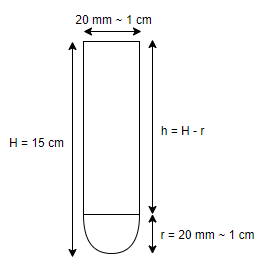
Now, let us find the height of the cylinder which is subtracting radius of hemisphere from given height of test tube
Now, on substituting the respective values we get,
Now, the volume of the cylinder is given by
Now, on substituting the respective values we get,
Now, on further simplification we get,
Let us now find the volume of the hemisphere which is given by
Now, on substituting the respective values we get,
Now, on further simplification we get,
Now, the capacity of the test tube is the sum of both volumes given by
Now, on further simplification we get,
Hence, the correct option is (b).
Note: It is important to note that the given value of diameter is in terms of a millimeter so when we use for our calculation we need to convert it into centimeter because if we substitute without conversion then the complete result would be incorrect.
It is also to be noted that the given height in the question is the total height of the test tube so to find the value of the volume of the cylinder in the upper part we need to find its corresponding height which is the difference between the height of the cylinder and the radius of the hemisphere in the bottom part.
Complete step by step answer:
RIGHT CIRCULAR CYLINDER:
A right circular cylinder is considered a solid generated by the revolution of a rectangle about one of its sides.
The volume of a cylinder is given by the formula is given by
HEMISPHERE:
A plane passing through the center of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
The volume of a hemisphere is given by the formula
Now, from the given conditions in the question we have
Here, given the value of the diameter as
As we already know the relation between radius and diameter we get,
As we already know the relation between cm and mm is given as
Now, on simplifying further simplification and converting to cm we get,

Now, let us find the height of the cylinder which is subtracting radius of hemisphere from given height of test tube
Now, on substituting the respective values we get,
Now, the volume of the cylinder is given by
Now, on substituting the respective values we get,
Now, on further simplification we get,
Let us now find the volume of the hemisphere which is given by
Now, on substituting the respective values we get,
Now, on further simplification we get,
Now, the capacity of the test tube is the sum of both volumes given by
Now, on further simplification we get,
Hence, the correct option is (b).
Note: It is important to note that the given value of diameter is in terms of a millimeter so when we use for our calculation we need to convert it into centimeter because if we substitute without conversion then the complete result would be incorrect.
It is also to be noted that the given height in the question is the total height of the test tube so to find the value of the volume of the cylinder in the upper part we need to find its corresponding height which is the difference between the height of the cylinder and the radius of the hemisphere in the bottom part.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




