Question

A thief in a stolen car passes through a police check post at his top speed of 90 km/h. A motorcycle cop, reacting after 2s, accelerates from rest at $5m/s^{2}$. His top speed is 108 km/h. Find the maximum separation between police and thief.
a. -112.5 m
b. 115 m
c. 116.5 m
d. None of these

Answer 1

Hint: This question has to be solved with an approach of relative motion because there are two different bodies in motion. However, we can also use the concept of differentiation as well. So we can use the property of maxima and minima in this problem.

Complete step by step answer:
Data,
 ${V_{\text{thief}}} = 90 \times \dfrac{5}{{18}} = 25m/s$
 ${V_{\text{cop}}} = 108 \times \dfrac{5}{{18}} = 30m/s$
${a_{\text{cop}}} = 5m/{s^2}$
When thief passes through check post

After 2s the cop reacts with accelerating his bike from rest.
At the same time the thief would have travelled a distance $ = 25 \times 2 = 50m$

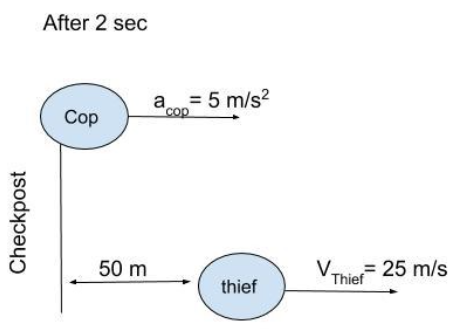
Now consider after some more time t, the distance between cop and the thief will be maximum.

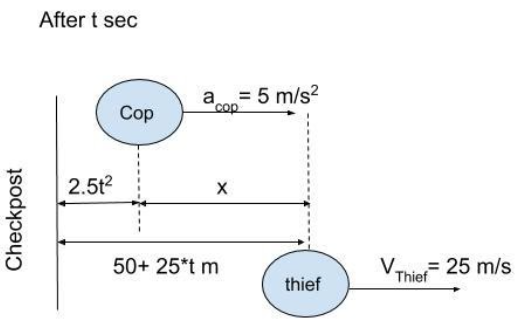
Hence, distance travelled by the thief after time t $ = 50 + 25 \times t$
Also the distance between the cop and the check post is given by,
$S = ut + \dfrac{1}{2}a{t^2}$
$S = 0 + \dfrac{1}{2}5{t^2} = 2.5{t^2}$

Let X be the max. difference between the cop and the thief, so we can write
$X = 50 + 25t - 2.5{t^2}$.......(1)
For maximum distance we can write,
\[\dfrac{{dX}}{{dt}} = 0\]
By putting values from equation 1 in the above equation, we get,
$25 - 5t = 0$
$t = 5\operatorname{s} $

Therefore, max. distance X can be found by puting the above value of t in equation (1)
$X = 50 + 25 \times 5 - 2.5 \times {5^2}$
$X = 112.5m$
Here the value in option A is the same but the sign is negative which is not the case with our solution. As there is no other option that agrees with our solution,so we will choose option D as our answer which is none of these.

Hence, the correct answer is option (A).

Note: Using the value $t=5s$ to find the value of velocity of cop we get,
${V_{cop}} = u + at = 0 + 5 \times 5 = 25m/s$
Which is equal to the velocity of the thief. So we can say that the max. separation between two bodies moving in the same direction with one body moving at constant velocity and other with uniform acceleration (as in the case of given problem) can be found by equating their velocities.