Question

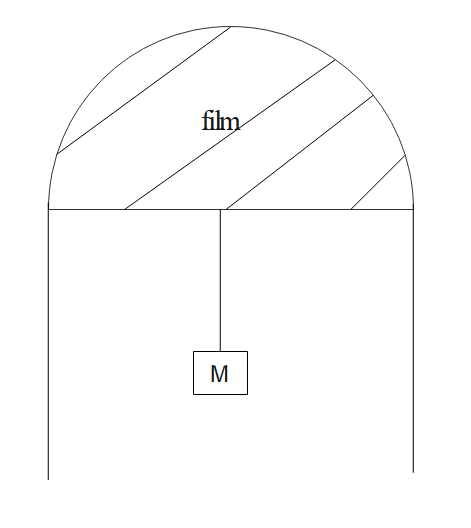
A thin liquid film formed between a u-shaped wire and light slider supports a weight of $1.5\times {{10}^{-2}}N$ (see figure). If the length of the slider 30cm and its weight negligible, then the surface tension of the liquid film is:

Answer 1

Hint: Find out the number of free surfaces present on the film surface. Next, calculate the force acting due to the weight balanced. Next, we know, force is equal to force acting per unit length. Therefore, calculate the surface tension acting on the liquid film easily.

Complete answer:
Given, the weight supported on the liquid film using the light slider. If we observe the case of liquid film, a liquid film will be having two free surfaces. Therefore, the surface tension of the liquid will be equal to,
$S.T=\dfrac{F}{2l}$
Here, the force acting on the light slider is equal to the weight of the box suspended,
$\begin{align}
  & \Rightarrow S.T=\dfrac{1.5\times {{10}^{-2}}}{2\times 30\times {{10}^{-2}}} \\
 & \Rightarrow S.T=0.025N{{m}^{-1}} \\
\end{align}$

So, the correct answer is “Option D”.

Additional Information:
The surface tension is a tendency of liquid surfaces to shrink into the minimum surface area possible. This phenomenon helps the insects usually denser than the water to float and slide on the water surface easily. At liquid air interfaces, surface tension results from the greater attraction of liquid molecules to each other than to the molecules in the air. There are mainly 2 primary mechanisms in play. One is the inward force on the surface molecules causing the liquid to contact. Second mechanism is that a tangential force parallel to the surface of the liquid is acted on the surface. The net effect results are the liquid that behaves as if its surface were covered with a stretched elastic membrane. Surface tension is an important factor in the phenomenon of capillarity.

Note:
In the above question, the length of the surface is taken as twice the length of the surface because the liquid in this case is having 2 free surfaces. The formula for surface tension is the ratio of force and the number of free surfaces. As the liquid in this case has 2 surfaces, we have multiplied the length twice. Even a bubble, precisely a soap bubble has 2 free surfaces one is the outside one and the second is the inside one.