Question

A thin straight infinitely long conducting wire having charge density $\lambda $ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.

Answer 1

Hint: Here, we are required to find the flux through the cylinder. Hence, we can use the Gauss’ Law. We know that Gauss's law requires the total charge enclosed which can be obtained using the linear charge density of the infinitely long wire. Here, the infinitely long wire suggests that the charge density will be uniform over the wire.

Formula Used:
Gauss law says that the electric flux through a closed surface is equal to the total enclosed charge divided by electrical permittivity of vacuum. The relation can be given as:
${{\phi }_{E}}=\dfrac{Q}{{{\varepsilon }_{0}}}$
Where, ${{\phi }_{E}}$= electric flux through a closed surface S whose Volume is $V$, $Q$ =total charge enclosed within $V$ and ${{\varepsilon }_{0}}$=electric constant.


Complete step by step answer:
Given that a thin straight infinitely long wire has a linear charge density $\lambda $.The electric field will be radial and perpendicular to the wire for this kind of configuration. On the flat surface of the cylinder, there will be no flux through the surface. The electric field (E) will remain constant at any point on the curved surface of the cylinder (as all points on it are equidistant from the wire) and perpendicular to it.

To find the electric flux through the cylinder, we use Gauss’s law. The charge enclosed by the cylinder $\lambda \times l$,as $l$ is the length of the cylinder and it is also the length of the charged wire within the cylinder. The charge is distributed uniformly on a thin straight conducting wire. Let q be the charge enclosed by the cylindrical surface.

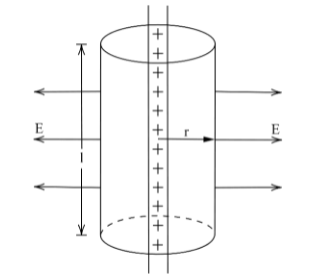
Linear charge density,
$\lambda =\dfrac{q}{l}$
$q=\lambda l.......(i)$
Gauss’s Theorem states that
$\text{Electric Flux=}\dfrac{\text{Net charge enclosed}}{{{\text{ }\!\!\varepsilon\!\!\text{ }}_{\text{0}}}}$
Total electric flux through the surface of cylinder
$\phi =\dfrac{q}{{{\varepsilon }_{0}}}[\because \text{Gauss's Theorem}]$
$\therefore \phi =\dfrac{\lambda l}{{{\varepsilon }_{0}}}$ [From eq. (i)]

Note: The electric flux in an area is equal to the multiplication of the electric field and the area of the surface projected in a plane which is perpendicular to the field. As we know, the electric field is perpendicular to the curved surface of the cylinder. So, the angle between the electric field and area vector is zero and $\cos \theta =1$