Question

A traffic signal board, indicating “SCHOOL AHEAD”, is an equilateral triangle with side “a”. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Answer 1

Hint: In order to use Heron’s formula for finding the area of the triangle, we need each side of the triangle. Use the property of equilateral triangle to find the sides of the triangle. And then use the formula directly or in modified form to find the area.

Complete step-by-step answer:

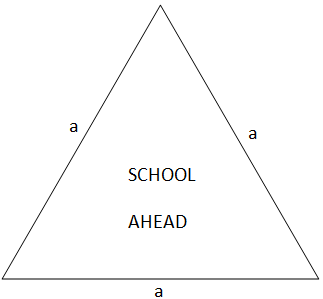
The sign board of the school is as shown in the figure. It has a shape of an equilateral triangle.
As we know that each side of the equilateral triangle is equal. So, let us consider the sides of the given triangle is “a”.
Given in the problem that perimeter = 180 cm
So sum of the sides = 180 cm
$
   \Rightarrow a + a + a = 180cm \\
   \Rightarrow 3a = 180cm \\
   \Rightarrow a = \dfrac{{180cm}}{3} \\
   \Rightarrow a = 60cm \\
 $
So, we have each side of the triangle.
Now, let us move to Heron’s formula.
According to Heron’s formula for general triangle with sides a, b, c
The area of the triangle is given by:
$A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Here S is the semi-perimeter given by:
$s = \dfrac{{a + b + c}}{2}$
Now, for the given triangle since we have
a = b = c = 60 cm
So, let use Heron’s formula and find the Area
$
   \Rightarrow s = \dfrac{{a + b + c}}{2} \\
   = \dfrac{{60cm + 60cm + 60cm}}{2} \\
   = \dfrac{{180cm}}{2} \\
   = 90cm \\
 $
Let us put the value of s in the equation of area
$
  A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \\
   \Rightarrow A = \sqrt {90\left( {90 - 60} \right)\left( {90 - 60} \right)\left( {90 - 60} \right)} c{m^2} \\
   \Rightarrow A = \sqrt {90 \times 30 \times 30 \times 30} c{m^2} \\
 $
Now let us simplify the part under the root to get the answer
$
   \Rightarrow A = \sqrt {9 \times 3 \times 3 \times 3 \times 10 \times 10 \times 10 \times 10} c{m^2} \\
   \Rightarrow A = 3 \times 3 \times 10 \times 10\sqrt 3 c{m^2} \\
   \Rightarrow A = 900\sqrt 3 c{m^2} \\
 $
Hence, the area of the signal board is $900\sqrt 3 c{m^2}$ .

Note: Heron's formula, named after the Hero of Alexandria, gives the area of a triangle when the length of all three sides is known. Unlike other triangle area formulas, there is no need to calculate angles or other distances in the triangle first. Also the direct formula for the area of the equilateral triangle could have been used which is $\dfrac{{\sqrt 3 }}{4}{a^2}$ . This formula can also be derived from Heron's formula.