Question

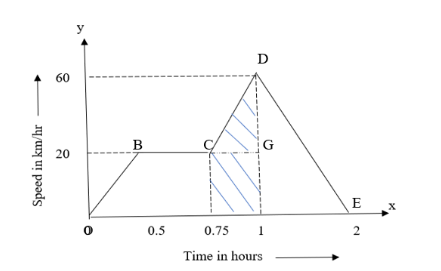
A train moves from one station to another in two hours time, it's speed during the motion is shown in the graph. Determine the maximum acceleration during the whole journey. Also calculate the distance covered during the time interval from 0.75 to 1.00 hour are

Answer 1

Hint: Acceleration is a rate of change of velocity with respect to time. In velocity v/s time graph it is nothing but the slope of the straight line connecting the points in a given time interval and displacement is the area under the curve of the velocity time graph over a given time interval.

Complete step by step answer:
Let us consider a train moving from one station to another station in one hour.

Now let us solve the first part of the problem i.e., we have to find the maximum acceleration.
Acceleration is nothing but rate of change of velocity w.r.t time, which is nothing but slope of the curve, and is given by
$a=\dfrac{\Delta y}{\Delta x}$ ….. (1)
So, to find the maximum acceleration we should find slope between two points successfully in the graph There are four such slopes they are- OB, BC, CD and DE.
Slope OB -
$\begin{align}
  & \Delta y=20-0=20 \\
 & \Delta x=0.5-0.25=0.25 \\
\end{align}$
Substituting in (1) we get
$a=\dfrac{20}{0.25}=800km/h{{r}^{2}}$

Slope BC –
$\begin{align}
  & \Delta y=0 \\
 & \Delta x=0.75-0.5=0.25 \\
\end{align}$
Substituting in (1) we get
$a=\dfrac{0}{0.25}=0km/h{{r}^{2}}$

Slope CD -
$\begin{align}
  & \Delta y=60-20=40 \\
 & \Delta x=1-0.75=0.25 \\
\end{align}$
Substituting in (1) we get
$a=\dfrac{40}{0.25}=1600km/h{{r}^{2}}$

Slope DE –
$\begin{align}
  & \Delta y=0-60=-60 \\
 & \Delta x=2-1=1 \\
 & \\
 & \therefore a=\dfrac{-60}{1}=-60km/h{{r}^{2}} \\
\end{align}$
From the above calculation it is clear that maximum acceleration =1600km/hr.
Now second part of the question: to find the distance covered during the time interval from 0.75 to 1.00 hour-
Distance covered is nothing but area under the curve in a given time interval, now to find the distance covered between 0.75 to 1.00 hour, consider area under it as shown in the above graph:
Distance covered=
Area between 0.75 and 1 hour = area of rectangle + area of triangle
$D=L\times B+\dfrac{1}{2}\times B\times H$
From the graph, L = 20, B = 0.25 and H = (60-20) = 40 on substituting we get

$\begin{align}
  & D=(20\times 0.25)+(0.5\times 0.25\times 40) \\
 & D=5+5 \\
 & D=10km \\
\end{align}$
D is the distance covered by an object in a given time interval.

Note: Students may make mistakes while calculating the height of the triangle by taking complete height, in the above example by taking 60 but it is wrong.
Height of the triangle is = total height of the area – height of the rectangle.
Slope of a line is the ratio of “vertical change” to the “horizontal change”
i.e., $\text{slope = }\dfrac{\Delta y}{\Delta x}$.