Question

A tree, which is 200m away from the pinhole, produces an image of height 1cm, in a pinhole camera of width 20cm. Find the height of the tree.
A) 30m
B) 20m
C) 10m
D) 40m

Answer 1

Hint: A pinhole camera is a camera which has no lens in it but has a tiny hole called the pinhole meaning a pin sized hole. The pinhole camera makes an inverted image and at the same time magnifies it as well. Here the image formed by the pinhole camera is inverted.

Complete step by step answer:
To find the height of the tree, we have been given:
Image size = 1cm;
Distance of the image = 20cm;
Distance of the object = 200m;
We have to find out:
The object size = h?

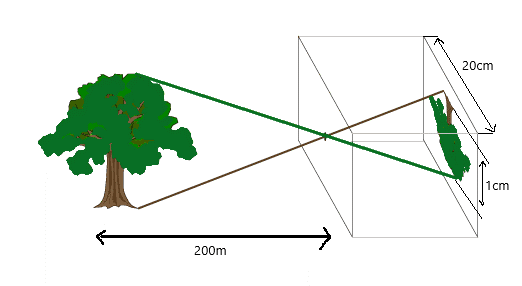
The image is taken from a pinhole camera so, the image would be magnified and the magnification of the formed image is given by the formula:
$\dfrac{{{\text{Image Size}}}}{{{\text{Object Size}}}} = \dfrac{{{\text{Distance of the image}}}}{{{\text{Distance of the object}}}}$ ;
Put the given value in the above equation:
$\dfrac{{1 \times {{10}^{ - 3}}}}{h} = \dfrac{{20 \times {{10}^{ - 3}}}}{{200}}$ ….(Here the object size (height) is taken as h )
Do the necessary calculation:
$ \Rightarrow \dfrac{{1 \times {{10}^{ - 3}}}}{h} = 1 \times {10^{ - 4}}$;
$ \Rightarrow 1 \times {10^{ - 3}} = h \times {10^{ - 4}}$;
The height of the tree is:
$\therefore h = 10m$;

Therefore, Option “C” is correct. The height of the tree is $10m$.

Note:
Here, there is no need to solve the question by applying trigonometric properties while considering the distance between the pinhole camera and the tree as a base and the length of the tree as the perpendicular length. Here, just apply the property of magnification of the pinhole camera.