
A triangle ABC with vertices A (-1, 0), B (-2, 3/4) and C (-3, -7/6) has its orthocenter H, then the orthocenter of the triangle BCH will be:
Answer
507.3k+ views
2 likes
Hint – In this question first draw perpendicular from vertices A, B and C (see figure) onto the sides BC, AC and AB respectively, then find the orthocenter of triangle ABC i.e. the coordinates of H, then form a triangle HBC and again draw perpendicular from vertices H, B and C onto the sides BC, HC and HB, this will help getting the orthocenter of the triangle HBC.
Complete step by step solution:
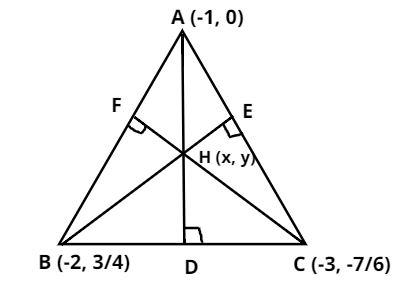
Consider the triangle ABC having vertices (-1, 0), (-2, 3/4) and (-3, -7/6).
Draw the perpendicular from the vertices on the line BC, AC and AB which cuts the line BC, AC and AB at the points D, E and F respectively
So the altitudes of triangles are AD, BE and CF as shown in figure, where altitudes are nothing but the perpendicular line.
So the orthocenter of the triangle is the intersection point of the altitudes.
Let orthocenter be H = (x, y).
So find out any two equations of the altitude and solve them which is the required orthocenter of the triangle.
Now to calculate the slope of the sides of the triangle. The formula to calculate the slope is given as,
Slope of a line =
To calculate the perpendicular slope of the sides of the triangle. It gives us the slope of the altitudes of the triangle. The formula to calculate the perpendicular slope is given as,
Perpendicular slope of a line =
To calculate the equation for the altitudes with their respective coordinates. The point-slope formula is given as,
Let A =
B =
C =
Therefore slope of line AB =
Therefore slope of altitude CF, (m) =
Therefore equation of line CF is
Now the line is passing through point C =
Now slope of line BC =
Therefore slope of altitude AD, (m1) =
Therefore equation of line AD is
Now the line is passing through point A =
Now from equation (1)
Now substitute this value in equation (2) we have,
Now simplify this equation we have,
Now substitute this value in equation (3) we have,
So the orthocenter of the triangle ABC is
H = (x, y) =
Now we have to find the orthocenter of triangle BCH.
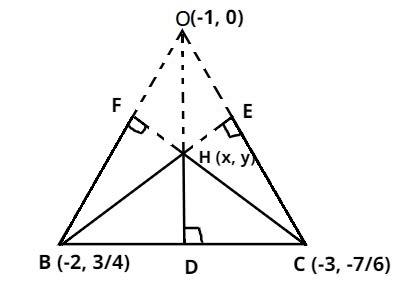
Now let the orthocenter of triangle BCH is O which is the intersection of the altitudes from the vertices of the triangle on the opposite sides of the triangle BCH.
As it is not possible to draw the altitudes on sides BH and CH internally so these altitudes are outside the triangle BCH as shown in figure 2, it meets a point O which is the required orthocenter of the triangle BCH as shown in the second figure.
Now as we see that the point O and the point A are the same, so the orthocenter of the triangle BCH is nothing but the coordinates of A.
So the orthocenter of the triangle BCH is = coordinates of A = (-1, 0)
So this is the required answer.
Hence option (D) none of these is the correct answer.
Note – The trick point here was that why have we drawn perpendiculars from different vertices. The reason behind this was by definition of orthocenter it is simply the intersection of the altitudes of the triangle, so we intended to find the equation of altitudes of triangles so that the point of intersection of them can be taken out. The concept of line that if two lines are perpendicular then their slopes are related as
Complete step by step solution:


Consider the triangle ABC having vertices (-1, 0), (-2, 3/4) and (-3, -7/6).
Draw the perpendicular from the vertices on the line BC, AC and AB which cuts the line BC, AC and AB at the points D, E and F respectively
So the altitudes of triangles are AD, BE and CF as shown in figure, where altitudes are nothing but the perpendicular line.
So the orthocenter of the triangle is the intersection point of the altitudes.
Let orthocenter be H = (x, y).
So find out any two equations of the altitude and solve them which is the required orthocenter of the triangle.
Now to calculate the slope of the sides of the triangle. The formula to calculate the slope is given as,
Slope of a line =
To calculate the perpendicular slope of the sides of the triangle. It gives us the slope of the altitudes of the triangle. The formula to calculate the perpendicular slope is given as,
Perpendicular slope of a line =
To calculate the equation for the altitudes with their respective coordinates. The point-slope formula is given as,
Let A =
B =
C =
Therefore slope of line AB =
Therefore slope of altitude CF, (m) =
Therefore equation of line CF is
Now the line is passing through point C =
Now slope of line BC =
Therefore slope of altitude AD, (m1) =
Therefore equation of line AD is
Now the line is passing through point A =
Now from equation (1)
Now substitute this value in equation (2) we have,
Now simplify this equation we have,
Now substitute this value in equation (3) we have,
So the orthocenter of the triangle ABC is
H = (x, y) =
Now we have to find the orthocenter of triangle BCH.
Now let the orthocenter of triangle BCH is O which is the intersection of the altitudes from the vertices of the triangle on the opposite sides of the triangle BCH.
As it is not possible to draw the altitudes on sides BH and CH internally so these altitudes are outside the triangle BCH as shown in figure 2, it meets a point O which is the required orthocenter of the triangle BCH as shown in the second figure.
Now as we see that the point O and the point A are the same, so the orthocenter of the triangle BCH is nothing but the coordinates of A.
So the orthocenter of the triangle BCH is = coordinates of A = (-1, 0)
So this is the required answer.
Hence option (D) none of these is the correct answer.
Note – The trick point here was that why have we drawn perpendiculars from different vertices. The reason behind this was by definition of orthocenter it is simply the intersection of the altitudes of the triangle, so we intended to find the equation of altitudes of triangles so that the point of intersection of them can be taken out. The concept of line that if two lines are perpendicular then their slopes are related as
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




