Question

A triangle with angle $A$ $15$degrees, and sides $AB=AC=10cm$, how do you find all the angles and sides of the triangle?

Answer 1

Hint: In this problem we need to calculate all the side lengths and angles in the given triangle by using the given data. In the given data we have the value of one angle and lengths of two sides. We can observe that the lengths of two sides are equal, which means the given triangle is an isosceles triangle. For an isosceles triangle we will be having two equal angles. So, we will assume that as $x$ and we will use the triangle property which is the sum of three angles in a triangle is equal to $180{}^\circ $ and calculate the values of the remaining two triangles. After that we have the all the angles and two sides, for the third side we will use the sine rule which is $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$. From this we will calculate the value of the remaining side.

Complete step by step answer:
Given that, A triangle has an angle $A$ of $15$ degrees, and sides $AB=AC=10cm$. The diagram of the triangle will be

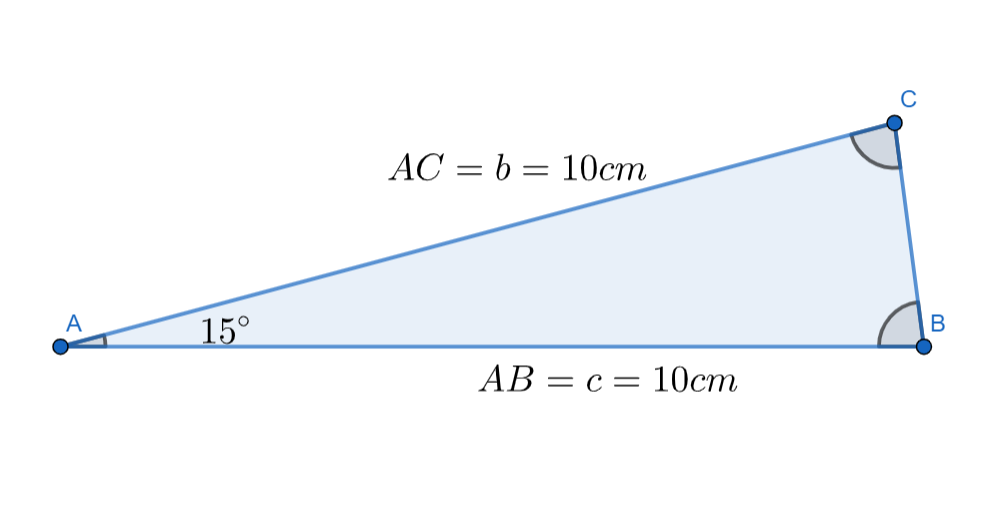
We can observe that the above triangle is an isosceles triangle. So, there must be two equal sides and two equal angles in the triangle. We have the two sides $AB=AC=10cm$. So, the angles $B$, $C$ must be equal.
Let use assume $\angle B=\angle C=x$. Then the sum of the all the interior angles in the triangle are
$\begin{align}
  & \angle A+\angle B+\angle C=15{}^\circ +x+x \\
 & \Rightarrow \angle A+\angle B+\angle C=2x+15{}^\circ \\
\end{align}$
We know that the sum of all the interior angles in the triangle are $180{}^\circ $. So, equating the above value to $180{}^\circ $, then we will get
$2x+15{}^\circ =180{}^\circ $
Simplifying the above equation by applying arithmetical operations, then we will have
$\begin{align}
  & 2x=180{}^\circ -15{}^\circ \\
 & \Rightarrow x=\dfrac{165{}^\circ }{2} \\
 & \therefore x=82.5{}^\circ \\
\end{align}$
Hence the value of remaining angles $B$, $C$ is $82.5{}^\circ $.
Now the diagram of the triangle with all the data we have will be
 

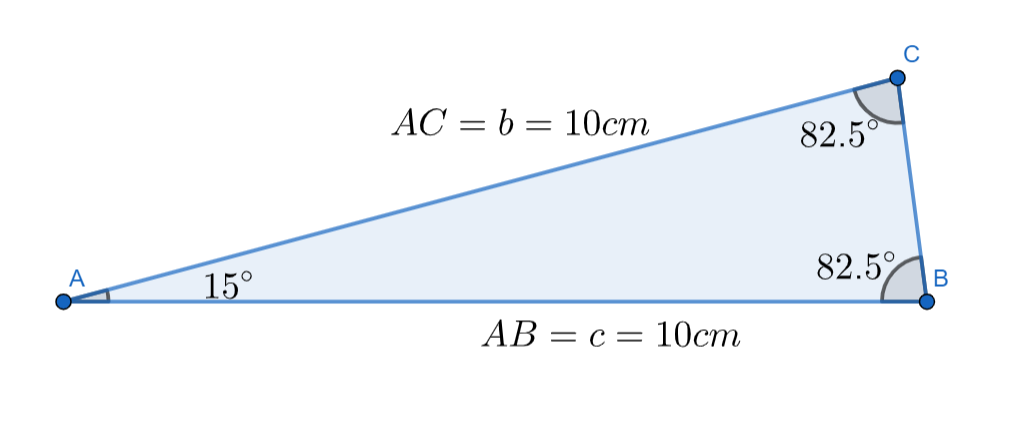
For the above triangle we are going to use the sine formula to calculate the length of third side. For this we are writing
$\begin{align}
  & \dfrac{a}{\sin A}=\dfrac{b}{\sin B} \\
 & \Rightarrow \dfrac{BC}{\sin 15{}^\circ }=\dfrac{10}{\sin 82.5{}^\circ } \\
 & \Rightarrow BC=\dfrac{10}{0.9914}\times 0.2588 \\
 & \therefore BC=2.61 \\
\end{align}$
Hence the length of the third side is $2.61$ centimetres.

Note: For this problem the above-mentioned method is the simple one and very easy if you remember the values of sine angles. There are different methods in geometry in which we need to construct a lot of things. So, we haven’t chosen that method because while construction the millimetre difference also may lead to the different answer.