Question

A triangular park has sides 120 m, 80 m and 50 m. A gardener has to put a fence all around it and also plant grass. How much area does he need to plant? Find the cost of fencing it with barbed wire at the rate of 20 per meter leaving a space 3 m wide for gate on one side.

Answer 1

Hint:In this question, we will find the area of a triangular park by using Heron’s formula. Then we will find the cost of fencing with barbed wire by calculating the perimeter of a park and subtracting it with the space for a gate that is 3 m on one side of a park.

Complete step-by-step answer:
The sides of the triangular park are 120 m, 80 m and 50 m.

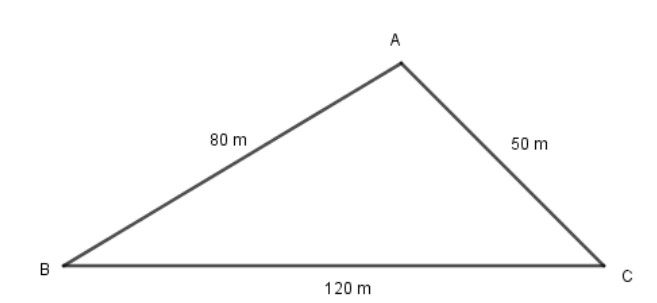
Perimeter of the triangular park = 120m + 80 m + 50 m= 250 m
Therefore, it's semi-perimeter (s) = 250/2 = 125 m
Now, we will use Heron’s formula to find the area of a triangle;
Area of a triangle = $\sqrt {s(s - a)(s - b)(s - c)} $
Here, a = 120 m, b = 80 m, c = 50 m, and s = 125 m
Now, putting these values in the above formula:
= $\sqrt {125(125 - 120)(125 - 80)(125 - 50)} $
$ = \sqrt {125 \times 5 \times 45 \times 75} $
$ = \sqrt {2109375} $
= 1452.36 sq. m
Hence, the gardener has to plant grass in 1452.36m²
Now we have to find the cost of fencing the field with a barbed wire at the rate of Rs. 20 per m leaving a space of 3m wide for a gate.
Therefore, the gardener has to fence = 250 – 3= 247m
So, total cost of fencing at the rate of Rs. 20 per meter = 247 × 20= Rs. 4940

Note:Heron’s formula is used when the length of all the sides of a triangle is given. Heron’s formula is equal to $\sqrt {s(s - a)(s - b)(s - c)} $ where s is the half of a perimeter of a triangle, and a, b, and c is the sides of a triangle.