Question

A truck is moving with a constant velocity of 54 kmph. In what direction should a stone be projected up with a velocity of 20 m/s, from the floor of the truck, so as to appear at right angles to the truck, for a person standing on earth?

Answer 1

Hint: By the definitions of scalar and vector quantities, All physical quantities can be classified into scalar and vector, wherein scalar quantities have only magnitude while vector quantities have direction too. Vectors cannot be operated with basic scalar operators.

Complete step by step answer:
The rate of change of distance per unit time is called speed. However, speed only represents the magnitude of the change of the distance with time but does not give an indication of the direction. Hence, it is a scalar quantity. So, we have another quantity velocity, which takes into consideration the direction in which the distance changes with respect to time, along with the magnitude.

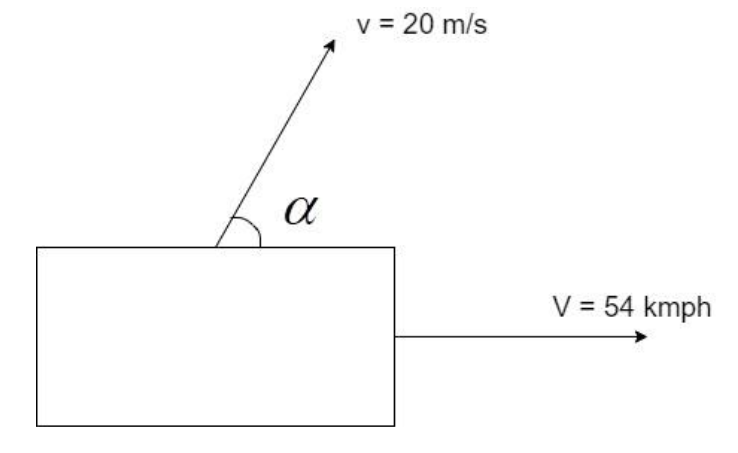
Consider the following setup with a truck moving at a constant velocity, V = 54 km/hr.
A stone is thrown off the truck with a velocity, v = 20 m/s with an angle of $\alpha $.
The velocity of the stone, v is considered a vector. It can be considered as a vector sum of its horizontal and vertical components, $v\cos \alpha $ and $v\sin \alpha $ as shown below:

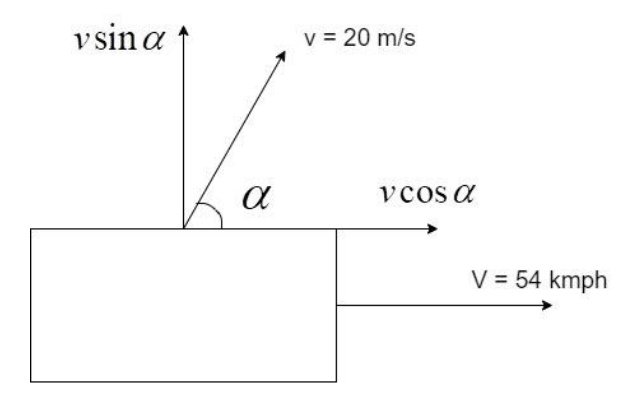
Here, we see that the component $v\sin \alpha $ is pointed in the upward direction and the other component $v\cos \alpha $ is pointed in the other direction.
For an observer on the ground, the relative velocity of the stone with respect to the truck, is given by:
${V_R} = V + v\cos \alpha $
Now, if the observer sees zero velocity in the horizontal direction, it means that the relative velocity, as stated above, is equal to zero.
$\therefore {V_R} = 0$

Substituting the values of the velocities, we get –
$V + v\cos \alpha = 0$
$ \Rightarrow 54 \times \dfrac{5}{{18}} + 20\cos \alpha = 0$
$ \Rightarrow 15 + 20\cos \alpha = 0$
$ \Rightarrow \cos \alpha = - \dfrac{{15}}{{20}}$
$ \Rightarrow \alpha = {\cos ^{ - 1}}\left( { - \dfrac{{15}}{{20}}} \right) = {\cos ^{ - 1}}\left( { - 0 \cdot 75} \right) = 138 \cdot {59^ \circ }$
Hence, the stone is projected at an angle of $138 \cdot {59^ \circ }$.

Note: The rate of conversion from one unit of velocity kilometre per hour to another unit metre-per-second is given as follows:
$1kmph = \dfrac{{1km}}{{1hr}} = \dfrac{{1000m}}{{3600\sec }} = \dfrac{5}{{18}}m{s^{ - 1}}$
Hence, 1 kmph is equal to $\dfrac{5}{18}^{th}$ of 1m/s.