Question

A truncated cone of solid rubber of mass $M$ is placed vertically. If its linear dimensions are shown in the figure and Y is Young's modulus of the cone, find the deformation of the cone.

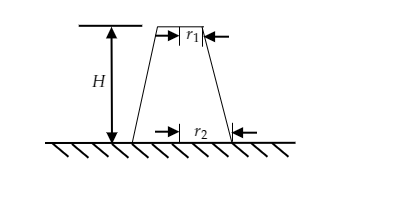
A) $\Delta l = \dfrac{{FH}}{{2\pi {r_1}{r_2}Y}}$
B) $\Delta l = \dfrac{{FH}}{{6\pi {r_1}{r_2}Y}}$
C) $\Delta l = \dfrac{{FH}}{{3\pi {r_1}{r_2}Y}}$
D) $\Delta l = \dfrac{{FH}}{{\pi {r_1}{r_2}Y}}$

Answer 1

Hint:Here to determine the deformation of the cone we have to derive an expression for the deformation in a small elemental area of the truncated cone based on the relation of Young’s modulus of a body. Then integrating that expression for the full height of the cone will provide us with the deformation of the entire cone.

Formulas used:
-Young’s modulus of a body is given by, $Y = \dfrac{{Fl}}{{A\Delta l}}$ where $F$ is the applied force, $A$ is the area of the body $l$ is the length of the body and $\Delta l$ is the change in length of the body.

Complete step by step answer.
Step 1: Sketch the truncated cone and consider an elemental area in it.

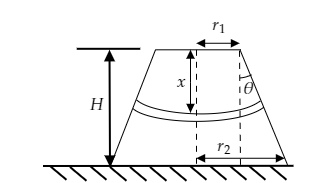
In the above figure, we consider a small elemental area of length ${\text{dx}}$ from the top of the cone. As seen in the above figure an angle $\theta $ is made at the top right corner of the cone.
Then we have $\tan \theta = \dfrac{{{r_2} - {r_1}}}{h}$ .
Also, the radius of the small element at $x$ distance can be expressed as $R = {r_1} + x\tan \theta $.
Then the area of the element will be $A = \pi {R^2} = \pi {\left( {{r_1} + x\tan \theta } \right)^2}$

Step 2: Express the relation for Young’s modulus for the small elemental area to obtain the required expression for the deformation ${\text{dl}}$ in the small element.
Young’s modulus of the small element can be expressed as $Y = \dfrac{{Fdx}}{{Adl}}$ ; ${\text{dl}}$ is the deformation of the small element of length ${\text{dx}}$.
$ \Rightarrow dl = \dfrac{{Fdx}}{{AY}}$ --------(1)
Substituting for $A = \pi {\left( {{r_1} + x\tan \theta } \right)^2}$ in equation (1) we get, $dl = \dfrac{{Fdx}}{{\pi {{\left( {{r_1} + x\tan \theta } \right)}^2}Y}}$ -------(2)

Step 3: Integrate equation (2) to obtain the deformation for the whole height of the cone.
The integral of equation (3) is expressed as $\Delta l = \int\limits_0^H {dl} = \int\limits_0^H {\dfrac{{Fdx}}{{\pi {{\left( {{r_1} + x\tan \theta } \right)}^2}Y}}} $
On integrating we have, $\Delta l = \dfrac{F}{{\pi Y}}\int\limits_0^H {\dfrac{{dx}}{{{{\left( {{r_1} + x\tan \theta } \right)}^2}}} = } \dfrac{F}{{\pi Y}}\left[ {\dfrac{1}{{{r_1} + x\tan \theta }} \times \dfrac{1}{{\tan \theta }}} \right]_0^H$
Substituting for $\tan \theta = \dfrac{{{r_2} - {r_1}}}{h}$ in the above expression we get,$\Delta l = \dfrac{F}{{\pi Y}}\left[ {\dfrac{H}{{H{r_1} + x\left( {{r_2} - {r_1}} \right)}} \times \dfrac{H}{{\left( {{r_2} - {r_1}} \right)}}} \right]_0^H$
Now applying the limits will give us $\Delta l = \dfrac{F}{{\pi Y}} \times \dfrac{H}{{{r_2} - {r_1}}}\left[ {\dfrac{1}{{{r_2}}} - \dfrac{1}{{{r_1}}}} \right]$
On simplifying we get, $\Delta l = \dfrac{{FH}}{{\pi {r_1}{r_2}Y}}$ .
Thus the deformation of the cone is $\Delta l = \dfrac{{FH}}{{\pi {r_1}{r_2}Y}}$ .

So the correct option is D.

Note:To avoid confusion while integrating equation (3) it is better if all the constant terms are taken outside the integral. In the integral $\int {\dfrac{{dx}}{{{{\left( {{r_1} + x\tan \theta } \right)}^2}}}} $, ${r_1}$ is a constant and so is $\tan \theta $ and so this integral is obtained using the formula$\int {\dfrac{{dx}}{{{{\left( {a + x\tan \theta } \right)}^2}}} = \dfrac{1}{{a + x\tan \theta }}} \times \dfrac{1}{{\tan \theta }}$ .