
A tuning fork with frequency
A.
B.
C.
D.
Answer
493.5k+ views
2 likes
Hint: Recall the expression for the resonant frequency of a tube with one closed end. This expression will relate the frequency to the number of harmonics, the speed of sound and the length of the tube at which the resonance is obtained. Rearrange the equation to express resonance lengths of the tube in terms of all the other parameters in the expression. Then, keeping in mind that the resonance tube forms only odd harmonics, rewrite the obtained equations in such a way that you can equate them to consequently obtain the speed of sound.
Formula used: Resonance frequency
Complete step by step answer:
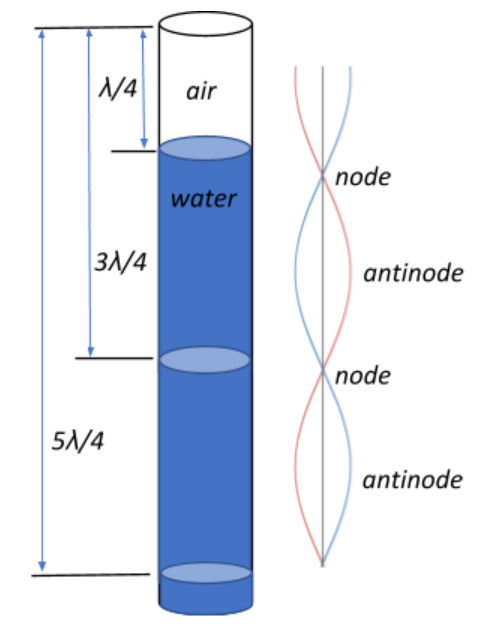
We know that acoustic resonance is a phenomenon wherein an acoustic system amplifies the sound waves whose frequency matches its own natural frequency of vibration.
A resonance tube with the lower end closed by water surface will have resonances at frequencies
Let the frequency of the tuning fork be
Subtracting the equations of the first two harmonics
In the question, we are given that
So, the correct answer is “Option D”.
Note: Remember that the expression for resonances of the resonance tube vary depending on the structure of the tube. The expression we used is only applicable for that tube that is closed on one end, and for open tubes it will thus be:
Also, the resonance properties of a resonance tube can be understood by considering the behaviour of a sound wave in air, which propagates via the compressions and rarefactions of the molecules of the medium. Within a tube, a standing wave is formed, with the closed end being the displacement node or the point of no vibration.
Formula used: Resonance frequency
Complete step by step answer:
We know that acoustic resonance is a phenomenon wherein an acoustic system amplifies the sound waves whose frequency matches its own natural frequency of vibration.
A resonance tube with the lower end closed by water surface will have resonances at frequencies
Let the frequency of the tuning fork be
Subtracting the equations of the first two harmonics
In the question, we are given that

So, the correct answer is “Option D”.
Note: Remember that the expression for resonances of the resonance tube vary depending on the structure of the tube. The expression we used is only applicable for that tube that is closed on one end, and for open tubes it will thus be:
Also, the resonance properties of a resonance tube can be understood by considering the behaviour of a sound wave in air, which propagates via the compressions and rarefactions of the molecules of the medium. Within a tube, a standing wave is formed, with the closed end being the displacement node or the point of no vibration.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




