Question

A uniform circular disk of mass 50 kg and radius 0.4 m is rotating with an angular velocity of $10rad{{s}^{-1}}$ about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in $rad{{s}^{-1}}$ ) of the system is:

Answer 1

Hint: Try to understand the system given in the question. We need to understand the property of the moment of inertia and conservation of angular momentum to solve this question.
Try to find the initial and final moment of inertia and then apply the law of conservation of angular momentum to solve the question.

Complete step by step answer:
Given, the mass of the uniform disk is, $M=50kg$
Radius of the disk, $R=0.4m$
The disk is rotating with an angular velocity, ${{\omega }_{i}}=10rad{{s}^{-1}}$

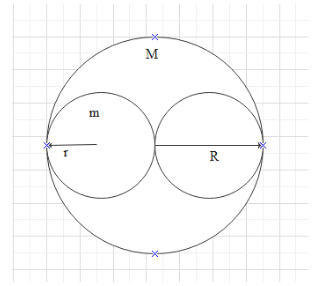
Now, we put two uniform circular rings, each of mass \[m=\text{ }6.25\text{ }kg\] and radius $r=0.2m$ , symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal.
Rings are at rest relative to the disk. So, we don’t have any external force or external torque on the disk.
To find the final angular velocity we will use the law of conservation of angular momentum.
Law of conservation of angular momentum gives that the initial and final angular momentum of the system is equal.
${{I}_{i}}{{\omega }_{i}}={{I}_{f}}{{\omega }_{f}}$
We know the value of initial angular velocity, and we can find out the moment of inertia of the initial and the final system.
So,
${{\omega }_{f}}=\dfrac{{{I}_{i}}{{\omega }_{i}}}{{{I}_{f}}}$
Now, moment of inertia of the uniform disk will be, ${{I}_{i}}=\dfrac{1}{2}M{{R}^{2}}$
Final moment of inertia of the system is, $\begin{align}
  & {{I}_{f}}=\dfrac{1}{2}M{{R}^{2}}+2\times \left( {{I}_{cm}}+m{{r}^{2}} \right) \\
 & {{I}_{f}}=\dfrac{1}{2}M{{R}^{2}}+2\times \left( m{{r}^{2}}+m{{r}^{2}} \right) \\
 & {{I}_{f}}=\dfrac{1}{2}M{{R}^{2}}+4\times m{{r}^{2}} \\
\end{align}$
Now,
$\begin{align}
  & {{\omega }_{f}}=\dfrac{{{I}_{i}}{{\omega }_{i}}}{{{I}_{f}}} \\
 & {{\omega }_{f}}=\dfrac{\dfrac{1}{2}M{{R}^{2}}\times 10}{\dfrac{1}{2}M{{R}^{2}}+4\times m{{r}^{2}}} \\
 & {{\omega }_{f}}=\dfrac{\dfrac{1}{2}\times 50\times {{0.4}^{2}}\times 10}{\dfrac{1}{2}\times 50\times {{0.4}^{2}}+4\times 6.25\times {{0.2}^{2}}} \\
 & {{\omega }_{f}}=\dfrac{40}{4+1} \\
 & {{\omega }_{f}}=\dfrac{40}{5} \\
 & {{\omega }_{f}}=8rad{{s}^{-1}} \\
\end{align}$
So, the final angular velocity will be, ${{\omega }_{f}}=8rad{{s}^{-1}}$.

Note: In this problem there is no external force or external torque is applied on the system. Because of the absence of any external force we can use the law of conservation of angular momentum on this system. Again, when solving this type of question always try to see if the units of the physical quantities are in the same measuring unit. If they are different then try to convert them to the same unit.