Question

A uniform horizontal meter scale of mass $m$ is suspended by two vertical strings attached to its two ends. A body of mass $2m$ is placed on the 75-cm mark. The tensions in the two strings are in the ratio
A. 1:2
B. 1:3
C. 2:3
D. 3:4

Answer 1

Hint:The meter scale is suspended by two vertical strings. The mass will be centered at 50cm. Thus, the tension of both the strings due to mass of the scale will be equal. The body of mass $2m$ is placed on the 75-cm mark. Therefore, there will be different tensions on the string. The difference in the value of two tensions of the strings will only be due to mass of the body.
Formula Used:
The tension in a string is: $T = mg$

Complete step by step solution:

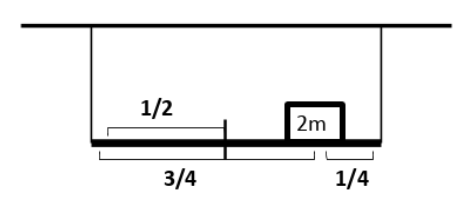
It is given in the problem that the meter scale has mass $m$and is suspended by two vertical strings. The center of mass of the meter scale will be at 50 cm (or$\dfrac{1}{2}$cm). It lies at the middle of the scale and is equidistant from both the strings, as both the strings are at the ends of the meter scale.
On the other hand, a body of mass $2m$ is placed on the 75-cm mark of the meter scale. That means that if mass $2m$ is placed at a distance of 75cm (or$\dfrac{3}{4}$cm) from string 1, then it is 25cm (or$\dfrac{1}{4}$cm) away from string 2.
The tension in the strings will be equal to the mass of the object times the gravitational force.
It is given by $T = mg$
Where, $m$ is the mass of the object and $g$ is the gravitational force.
Therefore tension in string 1 and string 2 will comprise the mass of the scale, mass of the object including the distance at which the object is from the string and the gravitational force acting on the object.
Thus, tension in string 1 is ${T_1} = mg\left( {\dfrac{1}{2}} \right) + 2mg\left( {\dfrac{3}{4}} \right) = \dfrac{{mg}}{2} + \dfrac{{6mg}}{4} = \dfrac{{8mg}}{4} = 2mg$
And tension in string 2 is ${T_2} = mg\left( {\dfrac{1}{2}} \right) + 2mg\left( {\dfrac{1}{4}} \right) = \dfrac{{mg}}{2} + \dfrac{{2mg}}{4} = \dfrac{{4mg}}{4} = mg$
Therefore, the tensions in the two strings are in the ratio
$\dfrac{{{T_2}}}{{{T_1}}} = \dfrac{{mg}}{{2mg}} = \dfrac{1}{2}$
Hence, option (A) is the correct answer.

Note: There is another method in which you can solve the given question and that is by balancing the torques acting about a point on the scale. We know that the scale is at rest. Therefore, it is in rotational equilibrium. This means torque about any end point of the scale is zero. Hence, calculate the toques due to the gravitational forces on the centre of mass and the two tensions and equate the net torque to zero.