Question

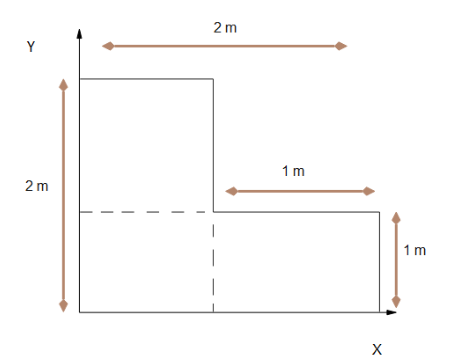
A uniform L shaped lamina with dimensions is shown. The mass of the lamina is $3$ kg. The center of mass of the lamina is:

Answer 1

Hint:To solve this we need to know the basic formulas of center of mass. In this problem we can see there are three discrete bodies each are rectangles. We have to find the center of mass of each and combine using the standard formula of center of mass , and we will get the answer.

Formula used:
Centre of Mass formula:
$X = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ....{m_n}{x_n}}}{{{m_1} + {m_2} + .....{m_n}}}$ and
$Y = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + ....{m_n}{y_n}}}{{{m_1} + {m_2} + .....{m_n}}}$


Complete step by step answer:
To make things simple we would consider the given body on a coordinate system. Now we can get the coordinates of the vertices of the given body. As the three laminas are uniform, by the help of the coordinates, we can see that the three laminas are squares , each of mass 1 kg. Let the center of mass of the three bodies Be C_1, C_2, C_3 respectively. As all three are square, their COM will be their mid points, thus
$C_1 = (\dfrac{1}{2},\dfrac{1}{2})$
$\Rightarrow C_2 = (\dfrac{3}{2},\dfrac{1}{2})$
$\Rightarrow C_3 = (\dfrac{1}{2},\dfrac{3}{2})$

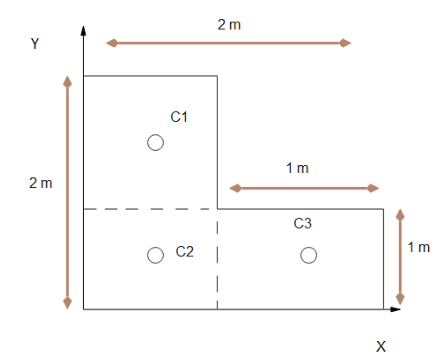
Now we have found the Center of mass of discrete bodies, now let’s apply the formula of Center of mass for a combined body :-
For X axis Center of mass:
$X = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + ....{m_n}{x_n}}}{{{m_1} + {m_2} + .....{m_n}}}$
$\Rightarrow X = \dfrac{{1.\dfrac{1}{2} + 1.\dfrac{3}{2} + 1.\dfrac{1}{2}}}{{1 + 1 + 1}}$
$\Rightarrow X = \dfrac{{\dfrac{1}{2} + \dfrac{3}{2} + \dfrac{1}{2}}}{3}$
$\therefore X = \dfrac{{2.5}}{3} = 0.833$
Now for Centre of mass along Y axis:
$Y = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + ....{m_n}{y_n}}}{{{m_1} + {m_2} + .....{m_n}}}$
$\Rightarrow Y = \dfrac{{1.\dfrac{1}{2} + 1.\dfrac{1}{2} + 1.\dfrac{3}{2}}}{{1 + 1 + 1}}$
$\Rightarrow Y = \dfrac{{\dfrac{1}{2} + \dfrac{1}{2} + \dfrac{3}{2}}}{3}$
$\therefore Y = \dfrac{{2.5}}{3} = 0.833$

Thus the centre of mass of the L shaped lamina of $3$ kg is at the point $(0.83,0.83)$.

Note:These questions require only the centre of mass formula to solve them and generally are very easy. It is important to remember the centre of mass formula for each body (students often get confused between the formulas of centre of mass). The more complex problems would require integrating the mass of the body, which we can do by considering a small strip from the body. We can also solve the given problem by method of integration.