Question

A uniform meter ruler of weight $2N$ is pivoted at the $60cm$ mark. A $4N$ load is suspended from one end, causing the ruler to rotate about the pivot. At the instant when the ruler is horizontal, what is the resultant moment about the pivot?
(A). $0Nm$
(B). $1.4Nm$
(C). $1.6Nm$
(D). $1.5Nm$

Answer 1

Hint: According to the principle of moments, the total anticlockwise torque must be equal to the clockwise torque at the equilibrium point. If the torques are not equal, a net torque acts on the body. Torque is the product of force and the distance from the axis of rotation. We can substitute corresponding values to calculate torque and then add or subtract according to the direction to find net torque.

Complete step by step solution:
In the experiment of calculating the mass of metre scale and the net torque acting on it, we will use the principle of moments as well as centre of gravity.
Centre of gravity is a point on the body on which the weight acts or appears to act. The metre scale has a uniform density hence; its centre of gravity will be in the middle of the ruler.
According to the principle of moments, an object is in a state of equilibrium if the sum of anticlockwise moments is equal to the sum of clockwise moments about the same pivot. If a metre ruler is balanced at any point the clockwise and anticlockwise moments must be equal.
Torque is given by-
$\tau =Fx$
Here, $\tau $ is the torque acting on a body
$F$ is the force acting on the body
$x$ is the distance from the axis of rotation

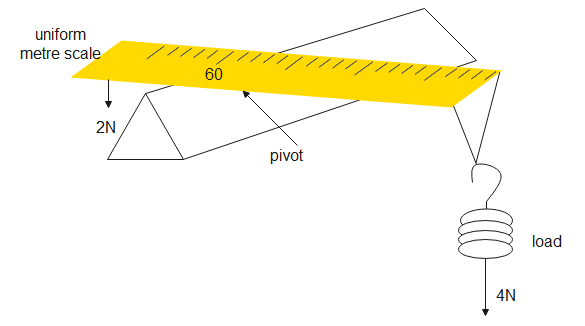
Given, weight of metre scale is $2N$, pivoted at $60cm$. Therefore, the axis of rotation is at $60cm$.
The centre of gravity is in the middle. Therefore, the centre of gravity is at $50cm$
Distance from axis of rotation- $60-50=10cm$. Substituting given values in the above equation, torque is-
${{\tau }_{1}}=2\times 10\times {{10}^{-2}}=0.2Nm$
Therefore, the torque due to weight of scale is $0.2Nm$ in the anticlockwise direction
Load of $4N$ is suspended at the end of scale, at $100cm$ or 1 metre mark. Distance from axis of rotation is $100-60=40cm$
Therefore, the torque will be-
${{\tau }_{2}}=4\times 40\times {{10}^{-2}}=1.6Nm$ in the clockwise direction.
Both moments are in different directions, so the net torque will be-
$\begin{align}
  & {{\tau }_{net}}=1.6-0.2 \\
 & \therefore {{\tau }_{net}}=1.4Nm \\
\end{align}$
Therefore, the net moment about the pivot is $1.4Nm$.
Hence, the correct option is (B).

Note: The direction of the torque is determined by the line joining the axis of rotation to the point of action. The net torque is in the direction of the greater torque so the scale will rotate in the direction of net torque. The pairs of forces due to which a torque acts on a body are known as moments.