Question

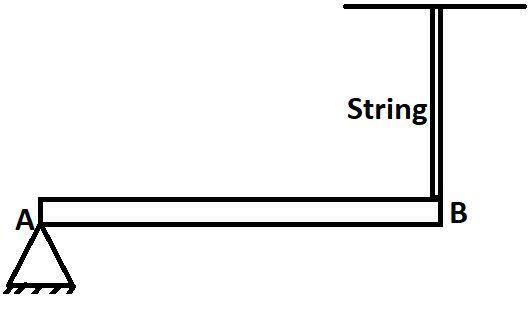
A uniform rod AB of mass 2kg is hinged at one end A. The rod is kept in the horizontal position by a massless string tied to point B. Find the reaction of the hinge (in N) on end A of the rod at the instant when the string is cut. ($g=10m/{{s}^{2}}$ )

Answer 1

Hint: At first we need to draw the diagram of the body when the string is cut. We have to show each and every force working on the body at that time. Now to find the reaction of the hinge just at the time of cutting the string. We have to find the torque about the point A and then we have to find the acceleration produced by the center of mass. Now with this value we apply it in the equation of force to find the required result.

Formulas Used:
$mg\times \dfrac{L}{2}=\dfrac{m{{L}^{2}}}{3}\times \alpha $
${{a}_{cm}}=\alpha \times \dfrac{L}{2}$

Complete step by step answer:
So, here according to the question, we come to know that the rod has a mass of 2kg. And the mass is hinged at one end that is at A.
On the other end the rod is held by a string in a horizontal position the string is massless.
Now according to the question when the string is cut,

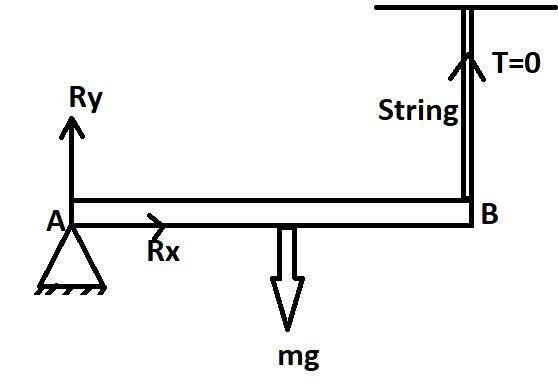
In the above diagram we consider that the string is cut, so we consider that the tension in the string T = 0 as there is no other body hanging with the help of string, now as the string is cut the bar should fall down with a force of (mg) and at point A two reaction forces are working one is Rx another one is Ry, now as in the motion of Rx there is no reaction so we are considering Rx as zero, but in case of Ry we see that there is a reaction of the bar falling down so,
Now to find the value of Ry we at first have to calculate the acceleration for the center of mass,
Now to find the acceleration of the center of mass we have to find angular acceleration of the rod,
Now, to find the angular acceleration we have to find the torque about point A,
Let the length of the rod be L,
So,
$mg\times \dfrac{L}{2}=\dfrac{m{{L}^{2}}}{3}\times \alpha $
On solving this,
$\alpha =\dfrac{3g}{2L}$ .
Now the acceleration produced by the center of mass will be,
 ${{a}_{cm}}=\alpha \times \dfrac{L}{2}$
${{a}_{cm}}=\dfrac{3g}{2L}\times \dfrac{L}{2}$
${{a}_{cm}}=\dfrac{3g}{4}$.
Now, if we apply the equation of force in vertical direction then,
$mg-Ry=\dfrac{3mg}{4}$
$Ry=\dfrac{mg}{4}$,
$Ry=\dfrac{2\times 10}{4}$,( we are placing the given values of ‘m’ and ‘g’)
$Ry=5N$
So, the reaction of the hinge (in N) on end A of the rod at the instant when the string is cut is 5N.

Note:
This question is very confusing and to find the force properly as we have to find the torque then from that torque the acceleration produced by the center of mass so it will be a bit tough to understand this process. In the equation $mg\times \dfrac{L}{2}=\dfrac{m{{L}^{2}}}{3}\times \alpha $, m is the mass of the rod, L is the length of the rod and $\alpha $ is the angular acceleration.