Question

A uniform rod AB of mass m and length 2a is falling freely without rotation under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed with which the rod begins to rotate is
$
A.\dfrac{v}{{2a}} \\
B.\dfrac{{4v}}{{3a}} \\
C.\dfrac{v}{{3a}} \\
D.\dfrac{{3v}}{{4a}} \\
 $

Answer 1

Hint: The question is taken from the system of particles and rotational motion and the concept of dynamics of rotational motion about the fixed axis should be known. The question is solved by conservation of angular momentum principle. This states that initial angular momentum is equal to final angular momentum.

Complete step by step answer:
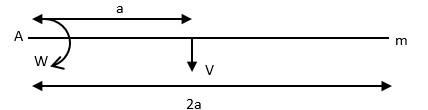
Considering a rod in this question it is given that the uniform rod AB which has a mass ‘m’ and length is ‘2a’, falls under the influence of gravity.

When it reached the speed ‘V’, it suddenly stopped at point ‘A’.

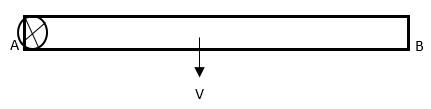
The rod rotates with ‘W’. We have to find the angular velocity.
Since, there is no torque about A (because it is punched), the angular momentum is conserved.

$\overrightarrow {{L_f}} = \left( {\dfrac{{m{L^2}}}{3}} \right)W $ (final angular momentum)
\[
  \overrightarrow {{L_i}} = (mv)r \\
   = (mv)\dfrac{L}{2} \\
  \overrightarrow {{L_f}} = \overrightarrow {{L_i}} \\
   \Rightarrow \left( {\dfrac{{m{L^2}}}{3}} \right)W = \dfrac{{mvL}}{2} \\
   \Rightarrow W = \dfrac{3}{2}\dfrac{V}{L} \\
 \]( By conservation of angular momentum)
Since,
$
  L = 2a \\
   \Rightarrow W = \dfrac{{3V}}{{2 \times 2a}} \\
  \boxed{W = \dfrac{{3v}}{{4a}}} \\
 $

So, the correct answer is “Option D”.

Note:
The angular momentum is conserved about the point ‘A’, hence initial angular momentum becomes equal to final angular momentum. Also remember that the concept of angular momentum is used in rotational motion. The concept of linear momentum as used in linear motion.