Question

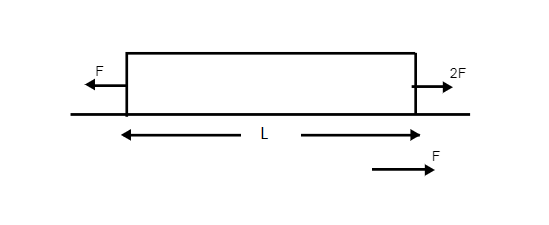
A uniform rod (area of cross section A. young’s modulus Y length L, mass M is pulled apart on a smooth horizontal surface as shown calculate the elongation of the rod after a long time.

Answer 1

Hint: When we applied force on the rod the total value of stress decreases as soon as it is moving away from the point of the application of the external force applied.
Formula used:
$\begin{align}
  & \Rightarrow F=ma \\
 & \Rightarrow \sigma =\dfrac{F}{A} \\
 & \Rightarrow Y=\dfrac{\sigma }{\varepsilon } \\
 & \Rightarrow \varepsilon =\dfrac{\delta }{L} \\
\end{align}$

Complete answer:
When we applied force on the rod the acceleration of the rod will be,
$a=\dfrac{F}{m}$
Now as to determine elongation of the rod let’s consider one small part of the rod as dx which is x distance away from the free end of the rod.
Now total value of the force in this section is,
$F'=\dfrac{F\times x}{L}....\left( 1 \right)$
Where, F = total force
F’ = force acts on dx section.
L = total length of the rod.
x = remaining length from dx.
Now let’s check stress on a small part dx by using the formula of the stress.
$\sigma =\dfrac{F'}{A}...\left( 2 \right)$
Where, $\sigma =$ stress
F’ = force
A = area of the rod
Now strain on the small part dx is
$\varepsilon =\dfrac{d\delta }{dx}...\left( 3 \right)$
Where, ε = strain
dδ = change in the length
dx = actual length
Now formula for the young’s modulus
$Y=\dfrac{\sigma }{\varepsilon }....\left( 4 \right)$
Now let’s substitute value of equation (2) and equation (3) in equation (4)
$\Rightarrow Y=\dfrac{F'}{A}\times \dfrac{dx}{d\delta }$
Substitute value of F’ in the equation,
$\begin{align}
  & \Rightarrow Y=\dfrac{F\times x}{LA}\times \dfrac{dx}{d\delta } \\
 & \Rightarrow d\delta =\dfrac{Fx}{LAY}dx \\
\end{align}$
Now let’s take integration on both sides,
$\begin{align}
  & \Rightarrow \int{d\delta }=\int{\dfrac{Fx}{LAY}}dx \\
 & \Rightarrow \delta =\dfrac{F}{LAY}\int{x\text{ }dx} \\
\end{align}$
Here we will take the integration limit from o to l.
$\begin{align}
  & \Rightarrow \delta =\dfrac{F}{LAY}{}_{O}\int{^{L}}x\text{ }dx \\
 & \Rightarrow \delta =\dfrac{F}{LAY}\left( \dfrac{{{x}^{2}}}{2} \right)_{o}^{L} \\
 & \Rightarrow \delta =\dfrac{F\times {{L}^{2}}}{2LAY} \\
 & \therefore \delta =\dfrac{FL}{2AY} \\
\end{align}$
Hence, elongation of the rod is $\dfrac{FL}{2AY}$ .

Note:
 In this solution we take stress and strain on the small part dx. So when you apply stress and strain formulas consider force on small part dx and deflection as part of dx.