Question

A uniform rod of weight $2.0\text{N}$ has a length of $80cm$. The rod is suspended by a thread $20cm$ from end X. A weight of $5.0\text{N}$ is suspended from end X. A student hangs a $6.0\text{N}$ weight on the rod so that it is in equilibrium. What is the distance of the $6.0\text{N}$ weight from end X?

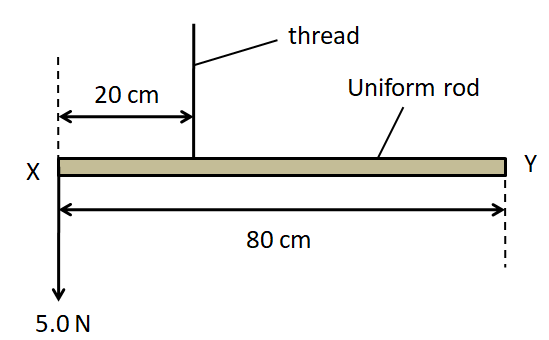
(A) $6cm$
(B) $10cm$
(C) $26cm$
(D) $30cm$

Answer 1

Hint To solve this question, we need to consider the vertical equilibrium of the given rod to determine the tension in the thread. Then, the consideration of the rotational equilibrium of the same rod will give out the required answer.

Complete step by step answer
Let the tension in the thread be $T$ and the distance of the $6.0\text{N}$ weight from end X be $y$, as shown in the below figure.

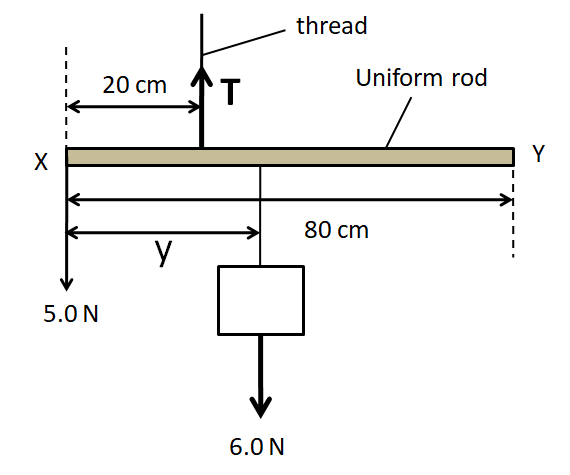
Now we consider the free body diagram of the rod.

We know that the weight of a body acts on its centre of gravity. As the centre of gravity of a rectangular uniform rod is located at its midpoint so the weight $2.0\text{N}$ is as shown above. Now, considering the vertical equilibrium of the rod, we get
$\Rightarrow T=5+6+2$
$\Rightarrow T=13N$ (1)
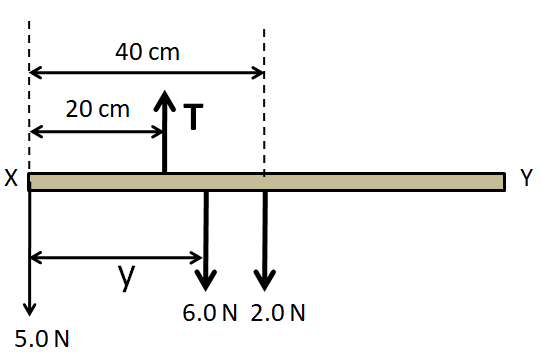
Now, we consider the rotational equilibrium of the rod at the end X of the rod. Summing up the moments of all the forces about the point X, we get
$\Rightarrow 5\left(0\right)+T\left(20\right)-6\left(y\right)-2\left(40\right)=0$ (Taking anticlockwise moments positive)
From (1)
$\Rightarrow 13\left(20\right)-6y-2\left(40\right)=0$
$\Rightarrow 6y=180$
Dividing both sides by $6$ we finally get
$\Rightarrow y=30cm$
Thus, the distance of the $6.0\text{N}$ weight from end X is equal to $30cm$.
Hence the correct answer is option D.

Note
We could have got the correct answer to this question even without determining the value of the tension in the thread also. We know that if a body is in rotational equilibrium, then the net torque about any point on it is equal to zero. Therefore, we can balance the torque at the point, where the rod is suspended by the thread so that the torque due to the force of tension in the thread would become zero. In this way we can solve these types of problems more quickly.