Question

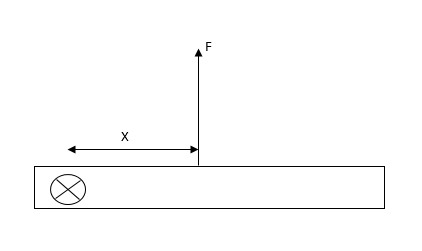
A uniform thin rod of length $L$ is hinged about one of its ends and is free to rotate about the hinge without friction. Neglect the effect of gravity. A force $F$ is applied to the rod. Find the normal reaction at the hinge as a function of $'x',$ at the initial instant when the angular velocity of rod is zero.

Answer 1

Hint: At the initial instant, the force applied on the red will be equal to the normal. So calculate linear acceleration of the rod above its moment of inertia and put it in the equation of force.


Formula used:
 $I = \dfrac{{M{L^2}}}{3}$
$\tau = I\alpha $
$F = ma$

Complete step by step answer:
 Observe the diagram.

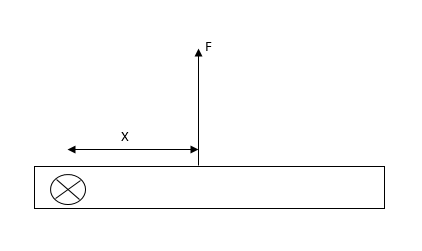
It is given that the length of the rod is $L$.
The rod is hinged at one end, where normal reaction is acting on the rod.
A force$F$ is applied on the rod at distance $x$ from the hinge.
Let mass of the rod be $M.$
Normal reaction and applied force are always perpendicular to the rod.
We can use the formula of the moment of inertia of rod about the axis passing through the end and perpendicular to it. Which is given by
$I = \dfrac{1}{3}M{L^2}$
Where$I$ is a moment of inertia.
$M$ is the mass of the rod.
$L$ is the length of the rod.
Now, rotation of the rod is done by applying force on it.
Therefore, for the rotation of rod,
Torque\[ = \]Force$ \times $perpendicular distance.
i.e.$\tau = xF$ . . . (1)
but we also know that
$\tau = I\alpha $ . . . (2)
Where,$\alpha $ is angular acceleration.
Form equation (1) and (2) we get
$I\alpha = xF.$
$ \Rightarrow \alpha = \dfrac{{xF}}{I}$
By putting the value of$I$in above equation, we get
$\alpha = \dfrac{{xF}}{{\dfrac{1}{3}M{L^2}}}$
$ \Rightarrow \alpha = \dfrac{{3xF}}{{M{L^2}}}$ . . . (3)
Now, for a rod of length $L$. Centre of mass will be at a distance $\dfrac{L}{2}$ from the end.
Therefore, $r = \dfrac{L}{2}$
Where,$r$is the distance of mid –point of rod from the end.
This $r$ will act as a radius of the circular path described by the centre of mass at the time of the rotation of the rod.
Now, linear acceleration is equal to the product of radius and angular acceleration.
i.e. $a = r\alpha $
where, $a$ is linear acceleration.
$r$ is radius
And $\alpha $ is angular acceleration.
By putting the valve of $r$and$\alpha $ in this equation, we get
$a = \dfrac{L}{2} \times \dfrac{{3xF}}{{M{L^2}}}$
$a = \dfrac{{3xF}}{{2M{L^2}}}$ . . . (4)
At initial instant normal reaction will be equal to the applied force.
i.e.$N = F = Ma$
$ \Rightarrow N = M \times \dfrac{{3xF}}{{2ML}}$ (from equation (4))
$ \Rightarrow N = \dfrac{{3xF}}{{2L}}$
Therefore, the normal reaction at the hinge as fraction of $x$, at the initial instant when the angular velocity of rod is zero, is $\dfrac{{3xF}}{{2L}}$

Note:
Multiple formulae are used in this question. Such questions cannot be solved easily if you try to think about the final answer. When you are at the first step. Best way is to think about one step at a time and develop a strategy as you move ahead.