
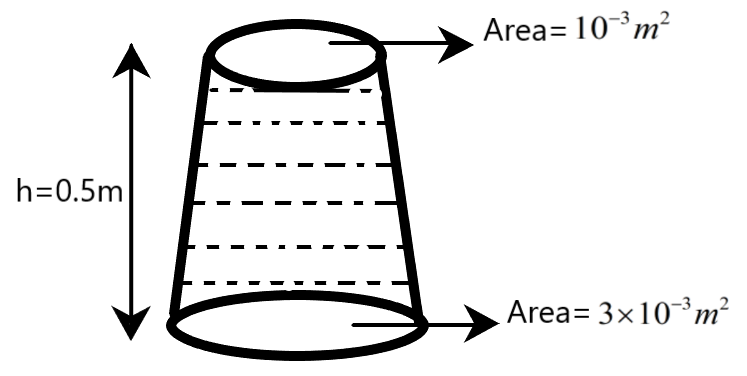
A uniformly tapering vessel shown in figure is filled with a liquid of density $1000kg{{m}^{-3}}$. The force that acts on the base of the vessel due to the liquid is (Take $g=10m{{s}^{-2}}$)
$\begin{align}
& A)15N \\
& B)8.4N \\
& C)9.12N \\
& D)12.37N \\
\end{align}$

Answer
576.6k+ views
Hint: Pressure is defined as force per unit area. Pressure on the base of a vessel containing liquid is also defined as the product of density of liquid, height of the liquid in the vessel and the acceleration due to gravity. Combining both these definitions, we can arrive at the pressure on the base of a vessel, containing liquid.
Formula used:
$1)P=\dfrac{F}{A}$
$2)P=\rho gh$
Complete answer:
We are provided with a uniformly tapering vessel, filled with a liquid of density $1000kg{{m}^{-3}}$, as shown in the following figure. From the figure, the area of top of the vessel is given as ${{10}^{-3}}{{m}^{2}}$ while the area of base of the vessel is given as $3\times {{10}^{-3}}{{m}^{2}}$.Also, the height of liquid in the tapering vessel is given to be $0.5m$. We are required to determine the force that acts on the base of the vessel due to the liquid.
We know that pressure is defined as force per unit area. Mathematically, pressure is given by
$P=\dfrac{F}{A}$
where
$P$ is the pressure on an area $A$ due to a force $F$
Let this be equation 1.
When we consider a vessel containing liquid, we also know that pressure on the base of the vessel is equal to the product of density of liquid, height of the liquid in the vessel and the acceleration due to gravity. If $P$ represents the pressure on the base of vessel, then, $P$ is given by
$P=\rho gh$
where
$\rho $ is the density of liquid filled in the vessel
$g$ is the acceleration due to gravity
$h$ is the height of liquid in the vessel
Let this be equation 2.
Combining equation 1 and equation 2, we have
$\dfrac{F}{A}=\rho gh$
Let this be equation 3.
Using equation 3, we can determine the force acting on the base of the given tapering vessel containing liquid as follows:
$\dfrac{F}{A}=\rho gh\Rightarrow F=A\rho gh=(3\times {{10}^{-3}}){{m}^{2}}\times 1000kg{{m}^{-3}}\times 10m{{s}^{-2}}\times 0.5m=15kgm{{s}^{-2}}=15N$
where
$A=3\times {{10}^{-3}}{{m}^{2}}$ is the area of base of tapering vessel, as provided in the question
$\rho =1000kg{{m}^{-3}}$ is the density of liquid filled in tapering vessel, as provided
$g=10m{{s}^{-2}}$ is the acceleration due to gravity, as provided
$h=0.5m$ is the height of liquid in tapering vessel, as provided
So, the correct answer is “Option A”.
Note:
Students need to notice that the area on top of the tapering vessel, as given in the figure, is irrelevant in the above problem. We are asked to determine the force acting on the base of the vessel, and not the force acting on the top of the vessel. Therefore, area of base of the vessel, density of the liquid and height of liquid in the vessel are the only important parameters to be used from the given diagram.
Formula used:
$1)P=\dfrac{F}{A}$
$2)P=\rho gh$
Complete answer:
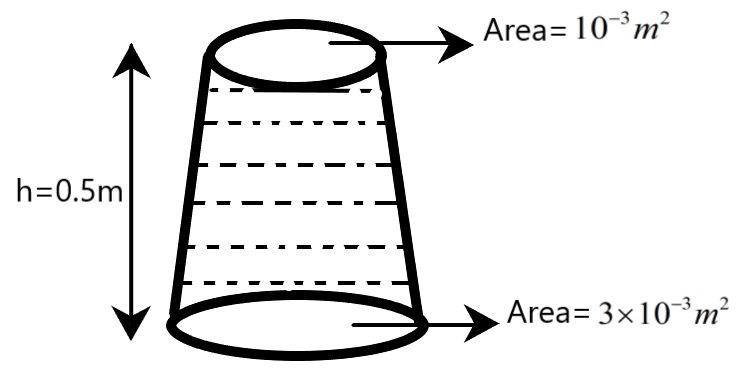
We are provided with a uniformly tapering vessel, filled with a liquid of density $1000kg{{m}^{-3}}$, as shown in the following figure. From the figure, the area of top of the vessel is given as ${{10}^{-3}}{{m}^{2}}$ while the area of base of the vessel is given as $3\times {{10}^{-3}}{{m}^{2}}$.Also, the height of liquid in the tapering vessel is given to be $0.5m$. We are required to determine the force that acts on the base of the vessel due to the liquid.

We know that pressure is defined as force per unit area. Mathematically, pressure is given by
$P=\dfrac{F}{A}$
where
$P$ is the pressure on an area $A$ due to a force $F$
Let this be equation 1.
When we consider a vessel containing liquid, we also know that pressure on the base of the vessel is equal to the product of density of liquid, height of the liquid in the vessel and the acceleration due to gravity. If $P$ represents the pressure on the base of vessel, then, $P$ is given by
$P=\rho gh$
where
$\rho $ is the density of liquid filled in the vessel
$g$ is the acceleration due to gravity
$h$ is the height of liquid in the vessel
Let this be equation 2.
Combining equation 1 and equation 2, we have
$\dfrac{F}{A}=\rho gh$
Let this be equation 3.
Using equation 3, we can determine the force acting on the base of the given tapering vessel containing liquid as follows:
$\dfrac{F}{A}=\rho gh\Rightarrow F=A\rho gh=(3\times {{10}^{-3}}){{m}^{2}}\times 1000kg{{m}^{-3}}\times 10m{{s}^{-2}}\times 0.5m=15kgm{{s}^{-2}}=15N$
where
$A=3\times {{10}^{-3}}{{m}^{2}}$ is the area of base of tapering vessel, as provided in the question
$\rho =1000kg{{m}^{-3}}$ is the density of liquid filled in tapering vessel, as provided
$g=10m{{s}^{-2}}$ is the acceleration due to gravity, as provided
$h=0.5m$ is the height of liquid in tapering vessel, as provided
So, the correct answer is “Option A”.
Note:
Students need to notice that the area on top of the tapering vessel, as given in the figure, is irrelevant in the above problem. We are asked to determine the force acting on the base of the vessel, and not the force acting on the top of the vessel. Therefore, area of base of the vessel, density of the liquid and height of liquid in the vessel are the only important parameters to be used from the given diagram.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE




