Question

A velocity of a projectile at the initial point A is $ \left( 2\hat{i}+3\hat{j} \right) $ m/sec . Its velocity in $ \left( m/\sec \right) $ at point B is:

(A) $ -2\hat{i}-3\hat{j} $
(B) $ -2\hat{i}+3\hat{j} $
(C) $ 2\hat{i}-3\hat{j} $
(D) $ 2\hat{i}+3\hat{j} $

Answer 1

Hint: As the projectile is moving in downward direction. Therefore the component reverses its direction and its sign changes. The x-component remains the same.

Complete step by step solution
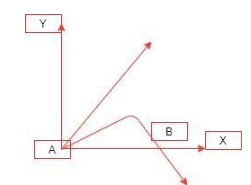
Consider that the projectile is fired from point A which is the initial point.
As the projectile moves, it covers distance along the horizontal due to the velocity of projection and along vertical in downwards direction due to the velocity attained under the effect of gravity.
Now, if we neglect friction due to air, then velocity of the projectile along horizontal will remain constant. So, the x component remains the same at point B, that is $ 2\hat{i} $ m/sec.
Now, when we talk about the motion along vertical, at point B the direction of y component changes and so the sign reverses, that is, it becomes $ -3\hat{j} $ m/sec.
So, the velocity at point B becomes $ \left( 2\hat{i}-3\hat{j} \right) $ m/sec.
So, the correct option is (C).

Note
Any object projected into space or air, such that it moves under the effect of gravity is called a projectile.
When projectile is fired parallel to horizontal, the equation of motion along horizontal is given as:
 $ \begin{align}
  & x=ut \\
 & t=\dfrac{x}{u} \\
\end{align} $
Motion along vertical is given by:
 $ \begin{align}
  & y=\dfrac{1}{2}g{{t}^{2}} \\
 & \text{ }=\dfrac{1}{2}g{{\left( \dfrac{x}{u} \right)}^{2}} \\
 & y=\dfrac{g{{x}^{2}}}{2{{u}^{2}}} \\
\end{align} $
When projectile is fired at an angle to horizontal equation of motion along horizontal is
 $ \begin{align}
  & x=\left( u\cos \theta \right)t \\
 & t=\dfrac{x}{u\cos \theta } \\
\end{align} $
Equation of motion along vertical is
 $ y=\left( u\sin \theta \right)t+\dfrac{1}{2}g{{t}^{2}} $
When a projectile is thrown vertically upwards with velocity u, The time of flight of such a projectile is given by $ T=\dfrac{2\text{ }u\sin 90{}^\circ }{8}=\dfrac{2u}{8} $
When a projectile is at the highest point of its trajectory,
It possesses velocity only along horizontal.
The velocity and acceleration of the projectile are perpendicular to each other.
A projectile possesses same horizontal range, when it is projected at
Angle $ \theta $ with horizontal angle $ \theta $ with vertical.
Angle $ \theta $ or $ 90{}^\circ -\theta $ with horizontal.
Angle $ \left( 45{}^\circ +\theta \right) $ or $ \left( 45{}^\circ -\theta \right) $ with horizontal.