Question

A veranda of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find:
(i) The area of the veranda.
(ii) The cost of cementing the floor of the veranda at the cost of Rs. 200 per sq. m.

Answer 1

Hint: To find the area of the veranda, we will need to find the dimensions of the veranda by considering its width. We will subtract the area of the room from the area of the room and veranda. After finding the area, we will multiply it by the cost per sq. m to find the total cost.

Complete step-by-step answer:
Let us draw a diagram to help us find the area.

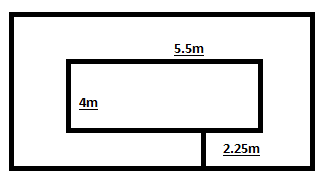
We will find the area of the veranda by subtracting the area of the smaller rectangle from the larger rectangle.
The dimensions of the inner rectangle are 5.5m $\times $ 4 m. Thus, the area of the rectangle is the product of length and width.
Area = Length $\times $ Width
$\begin{align}
  & \Rightarrow \text{Area = 4 }\times \text{ 5}\text{.5 sq}\text{. m} \\
 & \\
 & =22\text{ sq}\text{. m} \\
\end{align}$
To find the area of the larger rectangle, we must first find its dimensions. The length will be the length of the inner rectangle plus the length of the veranda.
Thus, Length = 5.5 + 2.25 + 2.25 m
$\Rightarrow \text{ Length = }10\text{ m}$
The width of the outer rectangle will be the width of the inner rectangle plus the width of the veranda.
Thus, Width = 4 + 2.25 + 2.25 m
$\Rightarrow \text{ Width = 8}\text{.5 m}$
Now, after finding the dimensions of the outer rectangle, we can find its area.
Area = Length $\times $ Width
$\begin{align}
  & \Rightarrow \text{ Area = }10\times 8.5\text{ sq}\text{. m} \\
 & \\
 & \text{=85 sq}\text{. m} \\
\end{align}$
Hence, the area of the veranda is the difference between the two areas.
Area = Outer Area – Inner Area
= 85 – 22 sq. m
= 63 sq. m
Thus, the area of the veranda is 63 sq. m.
Now, to find the cost of cementing the veranda, we must multiply the area of the veranda by the cost per sq. m which is Rupees 200.
Hence, Total Cost = Area $\times $ Cost per sq. m
= 63 $\times $ 200
= 12600
So the area of the veranda is 63 sq. m and the cost of cementing is Rs. 12600.

Note: There is another method to find the area of the veranda. We can split the veranda into four smaller rectangles, find their areas individually, and add them to get the total area. However, this method can be slightly longer and will involve more difficult calculations.