Question

A vertical stick 1 m long cast a shadow 50 cm long. At the same time, a tower casts a shadow 35cm. Determine the height of the tower.

Answer 1

Hint: First, find the ratio of the height of the vertical stick to its shadow. Now, find the ratio of the height of the tower to its shadow. Now, compare both the ratio and simplify the equation to determine the height of the tower.

Complete step-by-step answer:
To find:- The height of the tower.
Let the height of the tower be x.
The figure for the problem is,

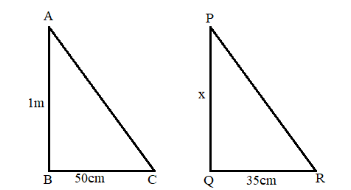
Now, find the ratio of the height of the vertical stick to its shadow,
\[Ratio = \dfrac{{1m}}{{50cm}}\]
Replace the height of the vertical stick from meter to centimeter,
\[Ratio = \dfrac{{100cm}}{{50cm}}\]
Cancel out the common factor from both numerator and denominator,
\[Ratio = 2\] …..(1)
Now, find the ratio of the height of the tower to its shadow,
$Ratio = \dfrac{x}{{35cm}}$ …..(2)
Compare both ratios and equate them,
$\dfrac{x}{{35cm}} = 2$
Cross multiply the equation,
$x = 70cm$
Hence, the height of the tower is 70cm.

Note: This can be done in another way.
To find:- the height of the tower.
Let the height of the tower be x.
The figure for the problem is,

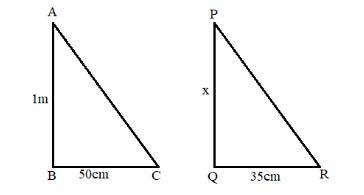
In $\Delta ABC$ and $\Delta PQR$,
$\angle B = \angle Q$ (right angle triangle)
Since the tower and the stick cast their shadows at the same time on the ground,
$\angle C = \angle R$
By AA similarity,
$\Delta ABC \sim \Delta PQR$
By CPCT,
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}}$
Substitute the values in the equation,
$\dfrac{{1m}}{{50cm}} = \dfrac{x}{{35cm}}$
Replace the height of the vertical stick from meter to centimeter,
$\dfrac{{100cm}}{{50cm}} = \dfrac{x}{{35cm}}$
Cancel out the common factor from both numerator and denominator,
$\dfrac{x}{{35cm}} = 2$
Cross multiply the equation,
$x = 70cm$
Hence, the height of the tower is 70cm.
Points to remember: The ratio should exist between the quantities of the same kind.
While comparing two things, the units should be similar.
There should be significant order of terms.
The comparison of two ratios can be performed, if the ratios are equivalent like the fractions.