Question

A vertical stick \[20{\text{ m}}\] long casts a shadow \[10{\text{ m}}\] long on the ground, at the same time a tower casts a shadow \[50{\text{ m}}\] long on the ground, the height of the tower is?
A) \[100{\text{ m}}\]
B) \[120{\text{ m}}\]
C) \[25{\text{ m}}\]
D) \[200{\text{ m}}\]

Answer 1

Hint: In this question we will first draw a rough figure. Then we will use the properties of similarities of triangles to make the two triangles similar. Then we will equate the ratio of their corresponding sides to find the height of the tower.

Complete step by step answer:
The given scenario is shown in the below diagram:

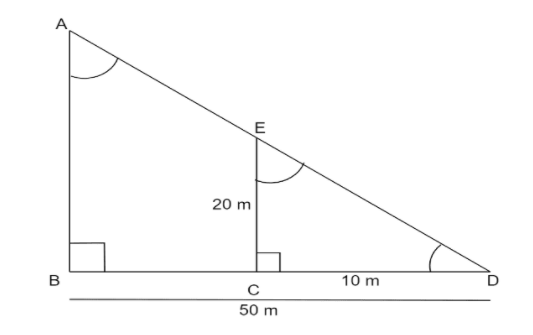
Let EC be the height of the stick and AB be the height of the tower.
The stick EC casts a shadow \[CD = 10{\text{ m}}\]
Tower casts a shadow \[BD = 50{\text{ m}}\]
Now we will try to make the two triangles i.e., \[\vartriangle ABD{\text{ and }}\vartriangle {\text{ECD}}\] similar.
In \[\vartriangle ABD{\text{ and }}\vartriangle {\text{ECD}}\] we see that,
\[\angle ABD = \angle ECD = {90^ \circ }\], since the tower and the stick both are vertical.
Also, we can see that;
\[\angle ADB = \angle EDC\], common angle
Since AB and EC are vertical lines on the same horizontal line, they are parallel to each other.
Hence, we get,
\[\angle BAD = CED\], corresponding angles
So, \[\vartriangle ABD \sim \vartriangle ECD\] by AAA similarity.
Now we know that if two triangles are similar then the ratio of their corresponding sides are equal.
So, according to this relation we get,
\[\dfrac{{AB}}{{EC}} = \dfrac{{BD}}{{CD}}\]
Now we will put the length of the sides. So, we have
\[ \Rightarrow \dfrac{{AB}}{{20{\text{ m}}}} = \dfrac{{50{\text{ m}}}}{{10{\text{ m}}}}\]
\[ \Rightarrow \dfrac{{AB}}{{20{\text{ m}}}} = 5\]
On simplification we get;
\[ \Rightarrow AB = 100{\text{ m}}\]

Therefore, the height of the tower is $100m$. So, Option (A) is correct.

Note:
One thing to note here is that when we write the ratios of the sides, we should choose the corresponding sides. For example, while solving the above question, we wrote \[\dfrac{{AB}}{{EC}} = \dfrac{{BD}}{{CD}}\].
But many students write it as \[\dfrac{{AB}}{{EC}} = \dfrac{{CD}}{{BD}}\], which is wrong. Since, in the LHS we put the side of triangle ABD in the numerator so in the RHS also we will have to keep the side of triangle ABD in the numerator. Another thing to note is that we should check whether the given dimensions are in the same unit or not.