Question

A vessel is in a conical shape. If its volume is 33.264 litres and height is 72cm, the cost of repairing its cross sectional area at Rs. 12 per sq.m is:
$
  {\text{A}}{\text{. 5}}{\text{.94}} \\
  {\text{B}}{\text{. 6}}{\text{.94}} \\
  {\text{C}}{\text{. 7}}{\text{.95}} \\
  {\text{D}}{\text{. None of these}} \\
$

Answer 1

Hint: To find the cost, we need to find the cross sectional area of the conical shape. Using the formula of the volume of a cone, we determine the radius of cone, we convert it into length and use it to find the cross sectional area.

Step-by-step answer:

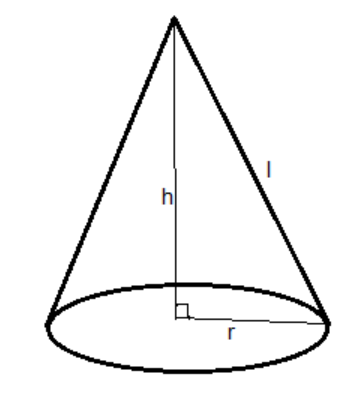
Given data,
Volume of conical shape is 33.264 litres and height is 72cm.
We know the volume of a cone of height h and radius r is given by V = $\dfrac{1}{3}\pi {{\text{r}}^2}{\text{h}}$
Given 33.264 litres, we know 1 litre = 1000 cm$^3$
Hence 33.264 × 1000 = 33264 cm$^3$

Using the given data we get,
$
   \Rightarrow 33264 = {\text{ }}\dfrac{1}{3}\pi {{\text{r}}^2}\left( {72} \right) \\
   \Rightarrow {{\text{r}}^2}{\text{ = }}\dfrac{{3 \times 33264}}{{72 \times \pi }} \\
   \Rightarrow {\text{r = }}\sqrt {441} = 21{\text{cm}} \\
    \\
$
We know the cross sectional area of a conical shape is given by πrl.
To find the value of length l, we observe the figure. We see height h and radius r are perpendicular to each other. Hence it forms a right angles triangle with hypotenuse as l.
Using Pythagoras theorem, we get
$
  {\text{l}} = {\text{ }}\sqrt {{{\text{r}}^2} + {{\text{h}}^2}} \\
   \Rightarrow {\text{l = }}\sqrt {{{21}^2} + {{72}^2}} \\
   \Rightarrow {\text{l = }}\sqrt {441 + 5184} = \sqrt {5625} \\
   \Rightarrow {\text{l = 75cm}} \\
$
Hence the cross sectional area of the cone = πrl = π × 21 × 75
                                                                                      = 4950 ${\text{c}}{{\text{m}}^2}$
We know, 1m = 100cm ⟹ 1${{\text{m}}^2}$= 10000${\text{c}}{{\text{m}}^2}$
Hence the cross sectional area of the cone = $\dfrac{{4950}}{{10000}}$= 0.495${{\text{m}}^2}$

Given, cost of repairing of cross sectional area is Rs.12 per sq.m
⟹Cost of repairing 0.495 sq.m = Rs. (0.495 × 12) = Rs. 5.94.
Hence Option A is the correct answer.

Note: In order to solve this type of problems the key is to know the formulae of the volume and cross sectional area of a conical figure. It is important that we observe we have to deduce the length, to find the cross sectional area. It is essential that all the values are in the same units while performing operations on them. Conversions of m to cm should be known.