Question

A wet open umbrella is held vertical and whirled about the handle at a uniform rate of 21 revolutions in 44s. If the rim of the umbrella is a circle of 1m in diameter and the height of the rim above the floor is 4.9m, the locus of the drop is a circle of radius.
$A.\quad \sqrt{2.5}m$
$B.\quad 1m$
$C.\quad 3m$
$D.\quad 1.5m$

Answer 1

Hint:
The problem is based on circular motion. The concepts of angular velocity $(\omega )$, tangential velocity $({{v}_{t}})$ etc. alongside a little bit of Newton's laws of motion is also required to solve this problem. The important formulas include, ${{v}_{t}}=\omega r$ and $s=ut+\dfrac{1}{2}a{{t}^{2}}$. Alongside these, making a diagram of the problem will be necessary to better understand and solve the problem.

Step by step solution:
Let’s start by making a diagram of the top view of the umbrella.

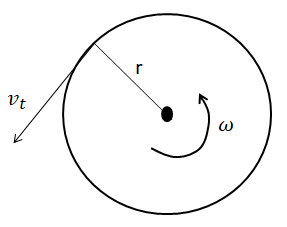
Given in the problem, we have the umbrella being whirled at 21 revolutions in 44s. Hence, the angular velocity of the umbrella is, $\omega =\dfrac{21\times 2\pi }{44}radian.{{s}^{-1}}=\dfrac{21\times 2(\dfrac{22}{7})}{44}radian.{{s}^{-1}}=\dfrac{21\times 2\times 22}{44\times 7}radian.{{s}^{-1}}\Rightarrow \omega =3radian.{{s}^{-1}}.$

The tangential velocity of the umbrella being whirled is given by, ${{v}_{t}}=\omega r,$ where r is the radius of the umbrella. We know that the circular rim of the umbrella has a diameter of 1m. Therefore, the radius is 0.5m.
Hence, the tangential velocity of the umbrella is, ${{v}_{t}}=3\times 0.5m{{s}^{-1}}=1.5m{{s}^{-1}}.$

Now, considering the drop, that falls from the edge of the rim to the floor, since the drop was at the edge of the rim, the drop was given horizontal velocity (which is the tangential velocity) only. Below is a diagram of the vertical view of the umbrella.

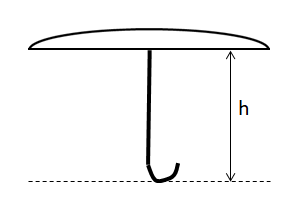
Hence, the drop was not having vertical velocity initially. ${{u}_{y}}=0.$ The height of the umbrella is 4.9m. The umbrella was standing on the ground. Hence, using the newton’s laws of motion, $s=ut+\dfrac{1}{2}a{{t}^{2}}$, which will be modified to $y={{u}_{y}}t+\dfrac{1}{2}g{{t}^{2}}$ for the current scenario.
That is, $4.9=0(t)+\dfrac{1}{2}(9.8){{t}^{2}}\Rightarrow 4.9=4.9{{t}^{2}}\Rightarrow t=\sqrt{1}s=1s.$

Hence, the time of flight for the drop is, 1s.
Now, let’s consider the drop travelling a distance x, before hitting the ground, from the time it left the umbrella. That flight time is equal to 1s, as found earlier. The locus of all such points at a distance x, from the perimeter of the umbrella will be another circle of radius R, taking the same center as that of the umbrella. Below is a diagram to understand better.

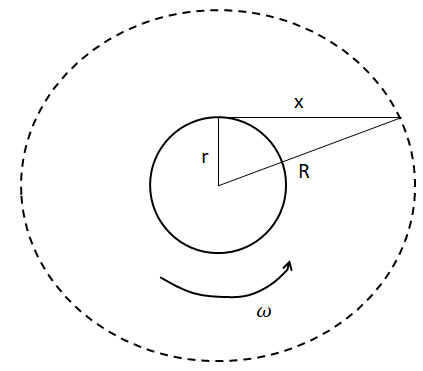
Here, a right angled triangle is formed, with R as the hypotenuse. (x) is the distance travelled by the drop before hitting the ground. The drop has horizontal velocity of ${{v}_{t}}=1.5m{{s}^{-1}}={{v}_{x}}.$
There isn’t any linear horizontal acceleration acting on the drop, hence, a=0. Hence using the Newton’s law of motion, $s=ut+\dfrac{1}{2}a{{t}^{2}}$ , which changes to $x={{v}_{x}}t=(1.5)(1)=1.5m.$

Using the Pythagorean theorem for the right angled triangle, ${{x}^{2}}+{{r}^{2}}={{R}^{2}}\Rightarrow {{R}^{2}}={{(1.5)}^{2}}+{{(0.5)}^{2}}\Rightarrow {{R}^{2}}=2.25+0.25\Rightarrow {{R}^{2}}=2.50\Rightarrow R=\sqrt{2.50}m$
Hence, the locus of all the drops will form a circle of radius $\sqrt{2.50}m.$

Note:
It’s necessary to make the diagram, so that you don’t make mistakes in making the right angled triangle towards the ending and don’t end up having wrong values for the wrong sides of the right angled triangle. The ending part, where the 2 consecutive circles are there with the common center is the part, where one should be more careful.