Question

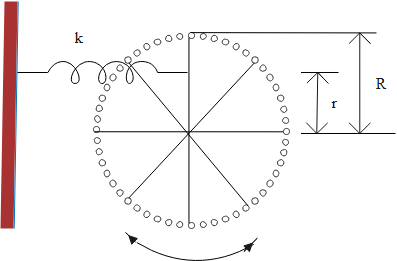
A wheel is free to rotate about its fixed axle. A spring is attached to one of its spokes a distance r from the axle, as shown in the above figure. (a) Assuming that the wheel is a hoop of mass m and radius R, what is the angular frequency v of small oscillations of this system in terms of m, R, r and the spring constant k? What is $$\omega$$ if (b) $$r=R$$ and (c) $$r=0$$ ?

Answer 1

Hint: Rotational energy and spring energy are forms of kinetic energy. The rotational energy is related to the wheel, whereas, the spring energy is related to the spring. We will find the expressions for the spring energy and the rotational kinetic emery. Then, we will equate both of the expressions to find the expression for the angular frequency.

Formula used:
 $$\begin{array}{rl}& I=M{R}^2\\ & K={\displaystyle \frac{1}{2}}I{\omega }^2\\ & \omega ={\displaystyle \frac{v}{r}}\end{array}$$

Complete step-by-step answer:
From the given information, we have the data as follows.
The radius of the wheel is, $$R$$
The distance between the centre of the wheel and the spring is, $$r$$
The spring constant is, $$k$$
The angular frequency is, $$\omega$$
The mass of the wheel is, $$m$$
In the case of the wheel, the rotational inertia is, $$I=M{R}^2$$ .
Where $$M$$ is the mass of the wheel and $$R$$ is the radius of the wheel.
In the case of the wheel, the rotational kinetic energy is computed as follows.
 $$K={\displaystyle \frac{1}{2}}I{\omega }^2$$
Where $$I$$ is the rotational inertia and $$\omega$$ is the angular frequency.
Now substitute the expressions of the rotational inertia and the angular frequency in the above equation.
 $$K={\displaystyle \frac{1}{2}}\left(M{R}^2\right){\left({\displaystyle \frac{v}{r}}\right)}^2$$
Here, $$v$$ is the tangential velocity of the point at which the spring is attached to one of the wheel’s spokes.
The spring energy is given as follows.
 $$E={\displaystyle \frac{1}{2}}k{x}^2$$
Where $$k$$ is the spring constant and $$x$$ is the distance between the centre of the wheel and the point at which the spring is attached to one of the wheel’s spokes.
 $$\Rightarrow E={\displaystyle \frac{1}{2}}k{r}^2$$
The energy will remain constant when the rotational kinetic energy equals the spring energy. So, we have,
 $$K=E$$
Substitute the expressions of the rotational kinetic energy and the spring energy in the above equation.
 $${\displaystyle \frac{1}{2}}(M{R}^2){\left({\displaystyle \frac{v}{r}}\right)}^2={\displaystyle \frac{1}{2}}k{r}^2$$
Represent the above expression in terms of the angular frequency.
 $$\begin{array}{rl}& {\displaystyle \frac{1}{2}}(M{R}^2){\left(\omega \right)}^2={\displaystyle \frac{1}{2}}k{r}^2\\ & \Rightarrow M{R}^2{\omega }^2=k{r}^2\end{array}$$
Therefore, the expression for the angular frequency is,
 $$\begin{array}{rl}& {\omega }^2={\displaystyle \frac{k{r}^2}{M{R}^2}}\\ & \Rightarrow \omega ={\displaystyle \frac{r}{R}}\sqrt{{\displaystyle \frac{k}{M}}}\end{array}$$
(a) The angular frequency v of small oscillations of this system in terms of m, R, r and the spring constant k is, $$\omega ={\displaystyle \frac{r}{R}}\sqrt{{\displaystyle \frac{k}{M}}}$$ .
When the radius of the wheel is equals the distance between the centre of the wheel and the spring, then, the angular frequency is,
 $$\begin{array}{rl}& \omega ={\displaystyle \frac{r}{R}}\sqrt{{\displaystyle \frac{k}{M}}}\\ & \Rightarrow \omega ={\displaystyle \frac{R}{R}}\sqrt{{\displaystyle \frac{k}{M}}}\\ & \therefore \omega =\sqrt{{\displaystyle \frac{k}{M}}}\end{array}$$
(b) The angular frequency $$\omega$$ if $$r=R$$ is $$\omega =\sqrt{{\displaystyle \frac{k}{M}}}$$ .
When the distance between the centre of the wheel and the spring equals zero, then, the angular frequency is,
 $$\begin{array}{rl}& \omega ={\displaystyle \frac{r}{R}}\sqrt{{\displaystyle \frac{k}{M}}}\\ & \Rightarrow \omega ={\displaystyle \frac{0}{R}}\sqrt{{\displaystyle \frac{k}{M}}}\\ & \therefore \omega =0\end{array}$$
(c) The angular frequency($\omega$) at $$r=0$$ is $$\omega =0$$ .

Note: The representation of the rotational energy of the wheel and the spring energy of the spring in terms of kinetic energy should be known. The equations of the rotational kinetic energy and the rotational kinetic energy can be equated if both, the wheel and the spring are told to be in motion.