Question

A whistle revolves in a circle with angular speed $\omega = 20$ rad per sec. using a string of length 50 cm. If the frequency of sound from the whistle is 385 Hz, then what is the maximum frequency heard by an observer who is for away from the centre $($velocity of sound $ = 340m/s)$

Answer 1

Hint:In a given problem the angular speed of whistle is given. So, first calculate the linear velocity of the whistle by using the following expression.
${v_S} = r\omega $
Also the frequency of sound from the whistle is given and velocity of sound is also given.
According to the Doppler effect, if a source is moving then the frequency is given by the following expression of the observer.
${f_0} = \left( {\dfrac{v}{{v + {v_S}}}} \right){f_S}$
Where
${f_0} = $ Frequency heard by an observer
${f_S} = $ Frequency of source
$v = $ Velocity of sound
${v_S} = $ Velocity of source
So, on putting the values in above expression, we will get frequency of observer.

Complete step by step answer:
Given that angular velocity of source whistle is $\omega = 20$ rad per sec.

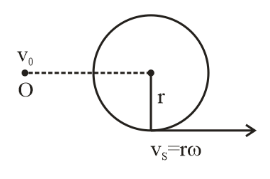
And the length of string $(\ell ) = 50cm$ this string revolves in a circle with a whistle.
So, $\ell = r = 50cm = 50 \times {10^{ - 2}}m$
So, linear velocity of source whistle is
$\Rightarrow {v_S} = r\omega = (50 \times {10^{ - 2}})(20)$
$\Rightarrow {v_S} = 1000 \times {10^{ - 2}}$
$\Rightarrow {v_S} = 10m/s$
According to Doppler effect, the frequency heard by observer is given by following expression
$\Rightarrow {f_0} = \left( {\dfrac{v}{{v + {v_S}}}} \right){f_S}$
Given that ${f_S} = 385Hz$
Velocity of sound $v = 340m/s$
$\Rightarrow {v_S} = 10m/s$
$\Rightarrow {f_0} = \left( {\dfrac{{340}}{{340 + 10}}} \right)385$
$\Rightarrow = \left( {\dfrac{{340}}{{350}}} \right)(385)$
$\Rightarrow = \dfrac{{34 \times 385}}{{35}}$
$\Rightarrow {f_0} = \dfrac{{13090}}{{35}}$
$\therefore {f_0} = 374Hz$

Hence, the maximum frequency heard by the observer is 374 Hz.

Note:
1. Observer Light source
     

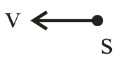
Frequency $f' = \left( {1 + \dfrac{v}{c}} \right)f$
Wavelength $\lambda ' = \left( {1 - \dfrac{v}{c}} \right)\lambda $ Violet shift
2. Observer Light source
    

Frequency $f' = \left( {1 - \dfrac{v}{c}} \right)f$
Wavelength $\lambda ' = \left( {1 + \dfrac{v}{c}} \right)\lambda $ Red shift