Question

A wire of resistance \[18\,{\text{Ohm}}\] is bent to form an equilateral triangle. The resistance across any two vertices of the equilateral triangle is (in Ohm):
A. 12
B. 6
C. 4
D. 9

Answer 1

Hint: Draw an equivalent circuit diagram of the given situation to determine the resistance across any two vertices of the equilateral triangle. Use the formula for the equivalent resistance for the resistors in series and parallel.

Formula used:
The equivalent resistance of the two resistors connected in series is
\[{R_S} = {R_1} + {R_2}\]
Here, \[{R_S}\] is the equivalent resistance, \[{R_1}\] is the resistance of the first resistor and \[{R_2}\] is the resistance of the second resistor.
The equivalent resistance of the two resistors connected in parallel is
\[\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]
Here, \[{R_P}\] is the equivalent resistance, \[{R_1}\] is the resistance of the first resistor and \[{R_2}\] is the resistance of the second resistor.

Complete step by step answer:
The equilateral triangle is a triangle in which all of its three edges are of the same length.
The total resistance across any wire is directly proportional to the length of the wire.
The total resistance of the given wire is \[18\,{\text{Ohm}}\].
The given wire is bent to form an equilateral triangle. Hence, the total resistance \[18\,{\text{Ohm}}\] of the wire is divided equally in three edges of the equilateral triangle.
Hence, the resistance through each edge of the equilateral triangle is \[\dfrac{{18\,{\text{Ohm}}}}{3} =
6\,{\text{Ohm}}\].
Now, calculate the resistance across any two vertices of the equilateral triangle.
The resistance across any two vertices of the equilateral triangle should be different as across any two vertices of the equilateral triangle two resistances are in series.
The diagram representing the resistances across 3 edges of the equilateral triangle and its equivalent circuit is as follows:

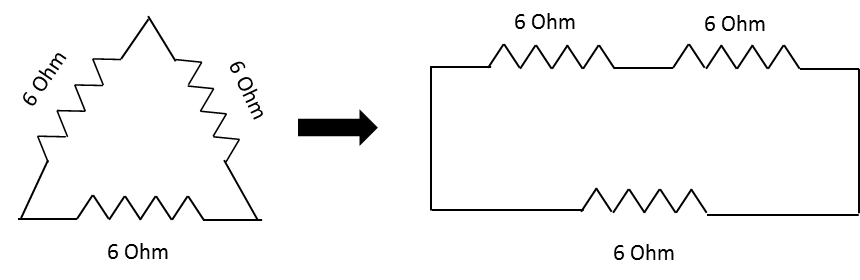
From the above diagram, it is clear that when a wire with resistance is bent into a equilateral triangle, its resistance divides equally in three edges of triangle and the its equivalent circuit across two vertices of the triangle contains resistance of the two edges of the triangle in series and resistance of one edge in parallel to them.
Let the two resistors in series be labeled \[{R_1}\] and \[{R_2}\] the third resistor in parallel to them is labeled\[{R_3}\].
Calculate the equivalent resistance \[{R_S}\] of the two resistances in series.
Substitute \[6\,{\text{Ohm}}\] for \[{R_1}\] and \[6\,{\text{Ohm}}\] for \[{R_2}\] in equation (1).
\[{R_S} = \left( {6\,{\text{Ohm}}} \right) + \left( {6\,{\text{Ohm}}} \right)\]
\[ \Rightarrow {R_S} = 12\,{\text{Ohm}}\]
Hence, the equivalent resistance across the two parallel resistors is \[12\,{\text{Ohm}}\].
Now, calculate the equivalent \[{R_P}\] resistance across the parallel resistance \[12\,{\text{Ohm}}\] and
\[6\,{\text{Ohm}}\].
Rewrite equation (2) for the equivalent resistance of the parallel resistances.
\[\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_S}}} + \dfrac{1}{{{R_3}}}\]
Substitute \[12\,{\text{Ohm}}\] for \[{R_S}\] and \[6\,{\text{Ohm}}\] for \[{R_3}\] in the above equation.
\[\dfrac{1}{{{R_P}}} = \dfrac{1}{{12\,{\text{Ohm}}}} + \dfrac{1}{{6\,{\text{Ohm}}}}\]
\[ \Rightarrow \dfrac{1}{{{R_P}}} = \dfrac{{6\,{\text{Ohm}} + 12\,{\text{Ohm}}}}{{\left( {12\,{\text{Ohm}}} \right)\left( {6\,{\text{Ohm}}} \right)}}\]
\[ \Rightarrow {R_P} = 4\,{\text{Ohm}}\]
Therefore, the equivalent resistance across any two vertices of the equilateral triangle is \[4\,{\text{Ohm}}\].

So, the correct answer is “Option C”.

Note:
One can also draw the equivalent circuit diagram with resistance of one edge in the upper arm and of two edges (in series) in the lower arm and do the needful calculations to determine the equivalent resistance. Both methods will result with the same option.