Question

(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent resistance of a group of resistance joined is parallel is equal to the sum of the reciprocal of the individual resistances.
(b) In an electric circuit two resistors of 12 \[\Omega \] each are joined in parallel to a 6 V battery. Find the current drawn from the battery.

Answer 1

Hint: In this question we have been asked to prove that, equivalent resistance of resistors in parallel, is equal to the sum of reciprocal of individual resistance of each resistor. Therefore, we shall use Ohm's Law to prove the same.
(b) We have been asked to calculate the voltage drawn from the battery of given readings. We shall use the Ohm's law, as it gives the relation of current, voltage applied and resistance.
Formula used:
\[V=IR\]

Complete answer:
(a) We have been asked to calculate the equivalent resistance of three resistors in parallel.
Therefore, let us consider three resistors with resistance connected in parallel as shown in the figure below.

      

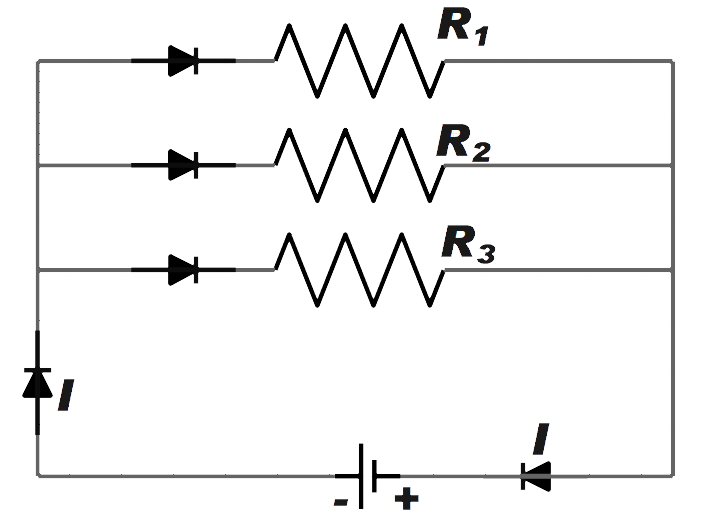
Let the total current in the circuit be I. The current through each branch will be \[{{I}_{1}},{{I}_{2}}\] and \[{{I}_{3}}\] .
Now we know that,
\[I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}\] …………………. (1)
We also know that voltage across each resistor in parallel connection is the same.
Therefore,
\[{{V}_{1}}={{V}_{2}}={{V}_{3}}=V\]
From Ohms law we can say that,
\[{{I}_{1}}=\dfrac{{{V}_{1}}}{{{R}_{1}}}\] ……………………. (2)
Similarly,
\[{{I}_{2}}=\dfrac{{{V}_{2}}}{{{R}_{2}}}\] ………………….. (3)
Also,
\[{{I}_{3}}=\dfrac{{{V}_{3}}}{{{R}_{3}}}\] …………………. (4)
Now, from (1), (2), (3) and (4)
We get,
\[I=\dfrac{{{V}_{1}}}{{{R}_{1}}}+\dfrac{{{V}_{2}}}{{{R}_{2}}}+\dfrac{{{V}_{3}}}{{{R}_{3}}}\]
But we know, \[{{V}_{1}}={{V}_{2}}={{V}_{3}}=V\]
Therefore,
\[\dfrac{V}{{{R}_{eq}}}=\dfrac{V}{{{R}_{1}}}+\dfrac{V}{{{R}_{2}}}+\dfrac{V}{{{R}_{3}}}\]
On solving,
We get,
\[\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}\]
Therefore, the reciprocal of the equivalent resistance of a group of resistance joined is parallel is equal to the sum of the reciprocal of the individual resistances.
Hence proved.

(b) It is given that two resistors are connected in parallel with a battery with voltage 6 V as shown in the figure below.

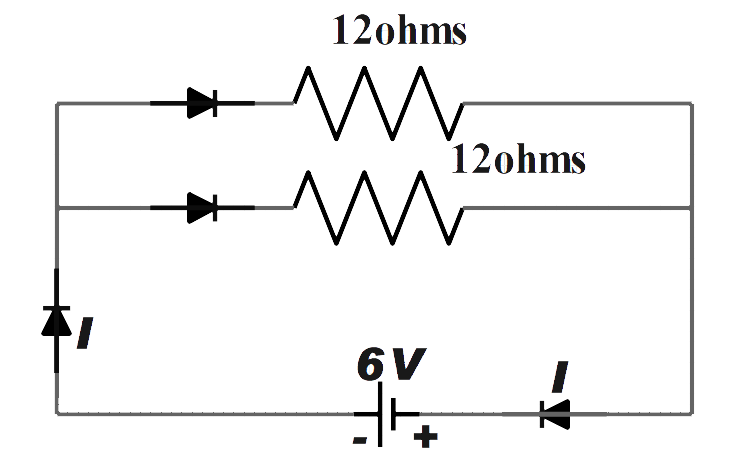
We have been asked to calculate the current flowing through the circuit.
Therefore, from Ohm's Law
We know
\[I=\dfrac{V}{{{\operatorname{R}}_{eq}}}\] ……………….. (A)
Therefore, calculating equivalent resistance
We know for parallel connections
\[\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}\]
Substituting values
\[\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{12}+\dfrac{1}{12}\]
On solving,
\[\dfrac{1}{{{R}_{eq}}}=\dfrac{2}{12}\]
\[{{R}_{eq}}=6\Omega \]
Therefore, substituting values in (A)
 We get,
\[I=\dfrac{6}{6}\]
Therefore,
\[I=1A\]
Therefore, the current through the resistor is 1 ampere.

Note:
Ohm's law states that current flowing through a circuit between two points is directly proportional to voltage across two points. The ohm's law is used to calculate the relation between voltage, current and resistance of the circuit. It states that current is directly proportional to voltage applied and inversely proportional to the resistance of the circuit.