
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 10cm and its base is of radius 3.5cm. Find the total surface area of the article.


Answer
523.8k+ views
Hint: As the hemispheres are scooped out, the total surface area will be different in this case. Try to find the curved surface area of the cylinder and two hemispheres using formula
Complete Step-by-Step solution:
In the given question we are given a wooden article which was made by scooping out a hemisphere from each end of a solid cylinder, with given information about dimensions given that the height of the cylinder is
In the figure it is drawn as
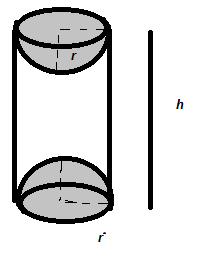
Here
We are asked to find the surface area of the figure of the cylinder with hemispheres scooped.
Instead of finding total surface area we will find their curved surface which will get the asked result.
So, the curved surface of the cylinder can be found using the formula
Curved surface area of cylinder
Here putting value of
The curved surface of the cylinder is
Now we will find curved surface area of ‘1’ hemisphere curve or surface on one of the end of cylinder using formula
Curved surface of
Substituting the values, we get
Here putting
For two hemispheres it will be,
Therefore the total area of wooden article will be sum of all the curved surface area so we get,
Total surface area
Note: Students should be well versed with the formulas of curved surface area of 3D figures, as they are used in the problems. They also should be careful about calculations to avoid many mistakes.
General mistake usually made by students is by seeing the total surface area in the question they apply the surface area formula which will give the wrong result.
Complete Step-by-Step solution:
In the given question we are given a wooden article which was made by scooping out a hemisphere from each end of a solid cylinder, with given information about dimensions given that the height of the cylinder is
In the figure it is drawn as

Here
We are asked to find the surface area of the figure of the cylinder with hemispheres scooped.
Instead of finding total surface area we will find their curved surface which will get the asked result.
So, the curved surface of the cylinder can be found using the formula
Curved surface area of cylinder
Here putting value of
The curved surface of the cylinder is
Now we will find curved surface area of ‘1’ hemisphere curve or surface on one of the end of cylinder using formula
Curved surface of
Substituting the values, we get
Here putting
For two hemispheres it will be,
Therefore the total area of wooden article will be sum of all the curved surface area so we get,
Total surface area
Note: Students should be well versed with the formulas of curved surface area of 3D figures, as they are used in the problems. They also should be careful about calculations to avoid many mistakes.
General mistake usually made by students is by seeing the total surface area in the question they apply the surface area formula which will give the wrong result.
Latest Vedantu courses for you
Grade 6 | CBSE | SCHOOL | English
Vedantu 6 Pro Course (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




