Question

A wooden ball of density D is immersed in water of density $ d $ to a depth $ h $ below the surface of water. Upto which height the ball will jump out of water when it is released?

Answer 1

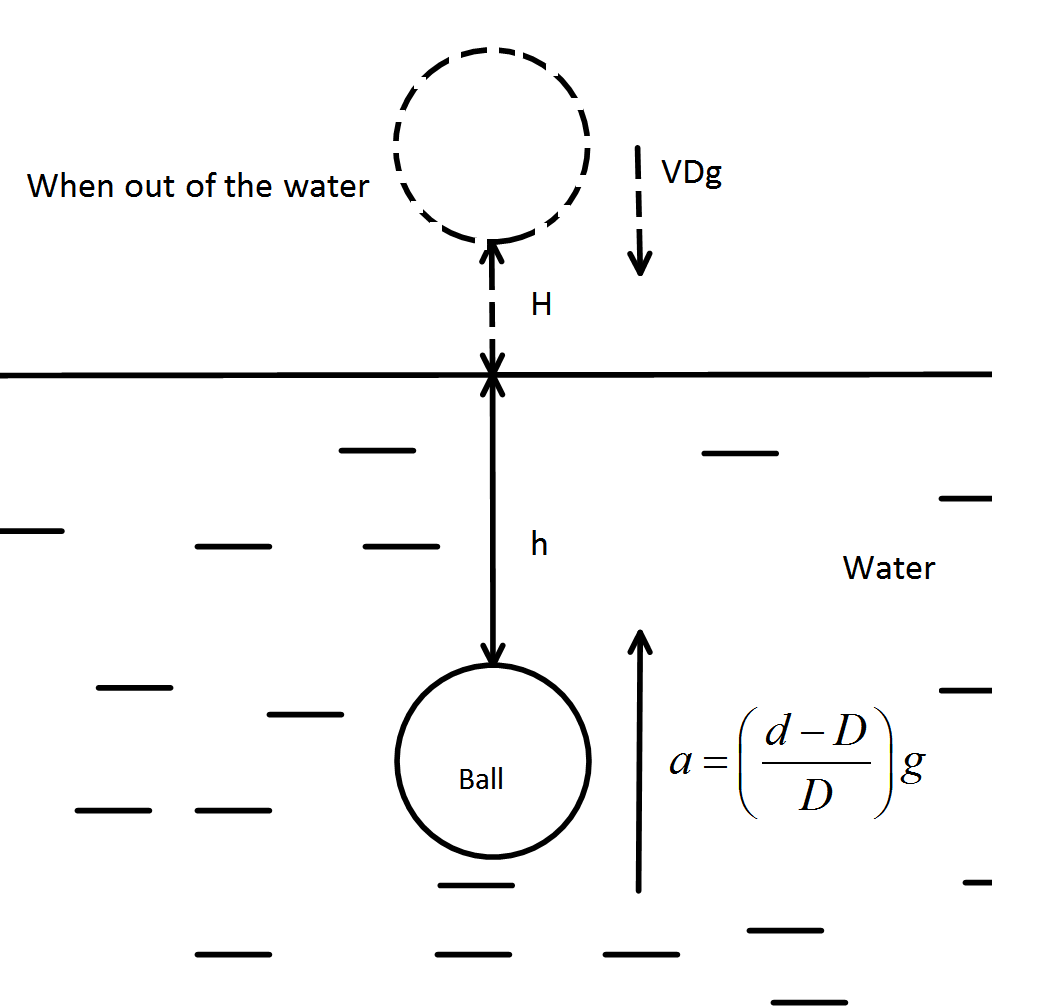
Hint :Write equation of motion of the ball to find the acceleration of the ball and use equations for 1D motion to find the height. Equation of motion of the ball can be written as $ VDa = Vdg - VDg $ where, $ VD $ is the mass of the ball. $ d $ is the density of water. $ VDg $ is the gravitational pull. $ Vdg $ is the upward buoyant force.

Complete Step By Step Answer:
We know the equation of motion of a body is given by, $ F = ma $ where $ F $ is the net unbalanced force and $ a $ is the acceleration of the body with mass $ m $ .
Here, the body is immersed, so, there will be an unbalance between the buoyant force and the gravitational pull which will rise to the acceleration of the ball.
Hence, we can write the equation of motion of the ball as, $ VDa = Vdg - VDg $ ,where, $ VD $ is the mass of the ball. $ d $ is the density of water. $ VDg $ is the gravitational pull. $ Vdg $ is the upward buoyant force.
Therefore, acceleration of the body is,
  $ a = \dfrac{{Vdg - VDg}}{{VD}} $
given, $ D $ is the density of wood and $ V $ is its volume
Hence, $ a = \left( {\dfrac{{d - D}}{D}} \right)g $ . (which is upwards and we take as the positive direction)

Now, from equation of 1D motion we have, $ {v^2} = {u^2} + 2as $
Here, we have given, $ u = 0 $ $ s = h $
Putting the values, we get the velocity of the ball at height $ h $ as,
 $ v = \sqrt {2ah} $ .
Now, when the ball comes out of the water, there is no buoyant force acting on it , there is only the gravitational pull which acts downwards hence, the acceleration of the ball is downwards outside the water.
so, again using, equation for 1D motion outside of the water,
we have, $ u = \sqrt {2ah} $ , $ v = 0 $ , $ a = - g $ and let the wood ball jumps a height $ H $ out of the water body.
So, putting the values we have,
 $ {0^2} = {(\sqrt {2ah} )^2} - 2gH $
 $ \Rightarrow 2ah = 2gH $
 $ \Rightarrow ah = gH $
Therefore we have , $ H = \dfrac{{ah}}{g} $
Putting the value of $ a $ we have,
 $ H = \dfrac{h}{g}\left( {\dfrac{{d - D}}{D}} \right)g $
 $ \therefore H = h\left( {\dfrac{{d - D}}{D}} \right) $
Hence, the ball will jump upto a height $ h\left( {\dfrac{{d - D}}{D}} \right) $.

Note :
If the force was balanced the wood ball would not have jumped out of the water, it would have stayed where it was as the force would have been balanced then. The jumped height depends on the density of the ball as the density increases and the jumped height of the block decreases. If the block density is greater than water then the block will not even come up, as the gravitational pull is greater than the buoyant force.